Set Partitioning

partition P(A)

no subset is an empty set
the union of all subsets equals the set A
the subsets are mutually exclusive, meaning they share no common elements (disjoint set)

Partitioning a set into two subsets is known as a bipartition.

Partitioning it into three subsets is called a tripartition.

A general partition into k subsets is referred to as a k-partition.

Note: There isn't a unique way to partition a set. A set of k elements can be divided into k! factorial partitions.

A Practical Example
Calculating the Number of Partitions
Observations

A Practical Example

Consider the finite set A consisting of 5 elements

$$ A = \{ 1,2,3,4,5 \} $$

An example of a partition is the following bipartition

$$ P(A) = \{ \ \{ 1,2,3 \} \ , \ \{ 4,5 \} \ \} $$

Using Euler-Venn diagrams, the bipartition is represented as follows:

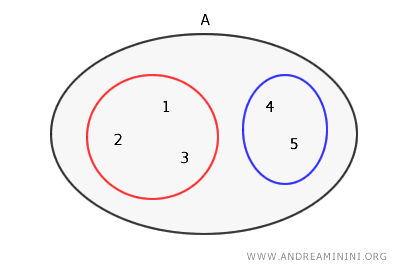
an example of bipartition

Verification: The partition consists of two non-empty subsets {1,2,3} and {4,5} that are disjoint $$ \{ 1,2,3 \} \cap \{4,5 \} = Ø $$ The union of the subsets equals the set A $$ \{ 1,2,3 \} \cup \{4,5 \} = \{ 1,2,3,4,5 \} = A $$

The set consists of 5 elements. Therefore, there are 52 possible partitions.

For instance, another partition is as follows. It is also a bipartition.

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3,4,5 \} \ \} $$

Another example is the following tripartition

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3,4 \} \ , \ \{ 5 \} \ \} $$

This is also a 4-partition because the set is divided into 4 subsets

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3 \} \ , \ \{ 4 \} \ , \ \{ 5 \} \ \} $$

In total, there are 52 possible combinations (partitions) of the elements within the set A.

Calculating the Number of Partitions

The number of partitions of a finite set $ A $ with $ n $ elements is given by the Bell number $ B_n $, which can be determined using the following recursive formula, with $ B_0 = 1 $ as the initial condition.

$$ B_n = \sum_{k=0}^{n-1} \binom{n-1}{k} B_k $$

In this formula:

$ \binom{n-1}{k} $ is a binomial coefficient (or combination), representing the number of ways to choose $ k $ elements from a set of $ n-1 $ elements.
$ B_k $ is the Bell number already calculated for sets with $ k $ elements.

The Bell number $ B_n $ represents the number of distinct ways a set of $ n $ elements can be partitioned into disjoint subsets.

Alternatively, the Bell number can be computed using Dobinski’s exponential formula:

$$ B_n = \frac{1}{e} \sum_{k=0}^{\infty} \frac{k^n}{k!} $$

In practice, the recursive formula is typically used for manual calculation, which allows us to find $ B_5 = 52 $ for the set $ A = \{ 1, 2, 3, 4, 5 \} $.

Example

Let’s calculate the number of partitions for the set $ A $, which contains $ n = 5 $ elements:

$$ A = \{ 1,2,3,4,5 \} $$

We’ll use the recursive formula:

$$ B_n = \sum_{k=0}^{n-1} \binom{n-1}{k} B_k $$

Given that $ n=5 $:

$$ B_5 = \sum_{k=0}^{5-1} \binom{5-1}{k} B_k $$

$$ B_5 = \sum_{k=0}^{4} \binom{4}{k} B_k $$

Starting with $ B_0 = 1 $ as the initial value of the recursive formula:

$$ B_0 = 1 $$

Now, let's calculate $ B_1 $:

$$ B_1 = \sum_{k=0}^{0} \binom{0}{k} B_k = \binom{0}{0} B_0 $$

In this case, we're summing only one term since the only possible $ k $ is 0.

$ \binom{0}{0} = 1 $, because there is exactly one way to choose 0 elements from a set of 0.
$ B_0 = 1 $, as defined initially.

Therefore:

$$ B_1 = 1 \times 1 = 1 $$

Next, we calculate $ B_2 $:

$$ B_2 = \sum_{k=0}^{1} \binom{1}{k} B_k = \binom{1}{0} B_0 + \binom{1}{1} B_1 $$

We compute each term:

$ \binom{1}{0} = 1 $, because there is one way to choose 0 elements from 1.
$ \binom{1}{1} = 1 $, because there is one way to choose 1 element from 1.

Substituting the values of $ B_0 $ and $ B_1 $:

$$ B_2 = 1 \times 1 + 1 \times 1 = 1 + 1 = 2 $$

Next, we calculate $ B_3 $:

$$ B_3 = \sum_{k=0}^{2} \binom{2}{k} B_k = \binom{2}{0} B_0 + \binom{2}{1} B_1 + \binom{2}{2} B_2 $$

We compute each combination:

$ \binom{2}{0} = 1 $, because there is one way to choose 0 elements from 2.
$ \binom{2}{1} = 2 $, because there are two ways to choose 1 element from 2.
$ \binom{2}{2} = 1 $, because there is one way to choose 2 elements from 2.

Substituting the values of $ B_0 $, $ B_1 $, and $ B_2 $:

$$ B_3 = 1 \times 1 + 2 \times 1 + 1 \times 2 = 1 + 2 + 2 = 5 $$

Now, we calculate $ B_4 $:

$$ B_4 = \sum_{k=0}^{3} \binom{3}{k} B_k = \binom{3}{0} B_0 + \binom{3}{1} B_1 + \binom{3}{2} B_2 + \binom{3}{3} B_3 $$

We compute each combination:

$ \binom{3}{0} = 1 $
$ \binom{3}{1} = 3 $, because there are three ways to choose 1 element from 3.
$ \binom{3}{2} = 3 $, because there are three ways to choose 2 elements from 3.
$ \binom{3}{3} = 1 $

Substituting the values of $ B_0 $, $ B_1 $, $ B_2 $, and $ B_3 $:

$$ B_4 = 1 \times 1 + 3 \times 1 + 3 \times 2 + 1 \times 5 = 1 + 3 + 6 + 5 = 15 $$

Finally, let's calculate $ B_5 $:

$$ B_5 = \sum_{k=0}^{4} \binom{4}{k} B_k = \binom{4}{0} B_0 + \binom{4}{1} B_1 + \binom{4}{2} B_2 + \binom{4}{3} B_3 + \binom{4}{4} B_4 $$

We compute each combination:

$ \binom{4}{0} = 1 $
$ \binom{4}{1} = 4 $, because there are four ways to choose 1 element from 4.
$ \binom{4}{2} = 6 $, because there are six ways to choose 2 elements from 4.
$ \binom{4}{3} = 4 $
$ \binom{4}{4} = 1 $

Substituting the values of $ B_0 $, $ B_1 $, $ B_2 $, $ B_3 $, and $ B_4 $:

$$ B_5 = 1 \times 1 + 4 \times 1 + 6 \times 2 + 4 \times 5 + 1 \times 15 = 1 + 4 + 12 + 20 + 15 = 52 $$

Thus, the Bell number is $ B_5 = 52 $.

In conclusion, there are 52 possible partitions for the set $ A = \{ 1,2,3,4,5 \} $ with 5 elements, calculated using the recursive formula and combinations.

Observations

The trivial partition
Every set X has a trivial partition that is the set itself $$ P(A) = \{ A \} $$
Example. Consider the set $$ A = \{ 1,2,3,4,5 \} $$ the trivial partition of set A is as follows $$ P(A) = \{ \ \{ 1,2,3,4,5 \} \ \} $$
The singleton partition
Every set X can have a partition consisting of single-element subsets (singletons) $$ P(A) = \{ \{ a_1 \} , \{ a_2 \} , ... \} $$
Example. Consider the set $$ A = \{ 1,2,3,4,5 \} $$ the singleton partition of set A is as follows $$ P(A) = \{ \ \{ 1 \} \ , \{ 2 \} \ , \{ 3 \} \ , \{ 4 \} \ , \{ 5 \} \ \} $$

And so on.