Upper and Lower Bounds

Exploring Upper and Lower Bounds

Given a set A and a subset B⊆A

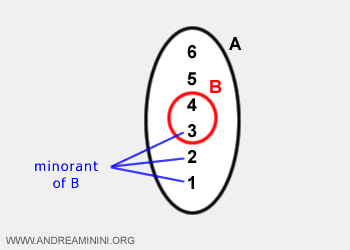
• An element k ∈ A is considered a lower bound (or minorant) of subset B if it is less than or equal to every element of subset B.

  Example. Take the set A = {1, 2, 3, 4, 5, 6} and the subset B = {3, 4}. The lower bounds of B are {1, 2, 3}
  

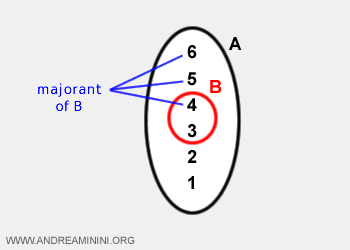
• An element k ∈ A is considered an upper bound (or majorant) of subset B if it is greater than or equal to every element of subset B.

  Example. For the set A = {1, 2, 3, 4, 5, 6} and the subset B = {3, 4}, the upper bounds of B are {4, 5, 6}
  

Range of Upper and Lower Bounds a Set Can Have

A set may possess multiple or no upper and lower bounds.

Practical Examples

Some sets are characterized by having lower bounds but lacking upper bounds.

These are referred to as sets bounded below.

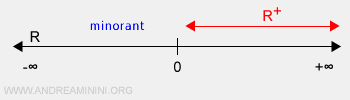
Example of a set without upper bounds. The set of positive real numbers R⁺, an infinite collection within the interval (0,+∞), belongs as a subset of the real numbers R. It includes lower bounds like zero and all negative real numbers, even though such bounds do not fall within R⁺ itself. For instance, zero is not a member of R⁺, and there exist infinitely many real numbers between zero and any positive real number. Additionally, R⁺ lacks upper bounds due to its unbounded nature above +∞.

Conversely, some sets present upper bounds yet no lower bounds.

These sets are known as sets bounded above.

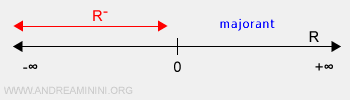
Example of a set lacking lower bounds. The set of negative real numbers R^- forms an infinite set within the range (-∞,0), acting as a subset of the real numbers R. It has upper bounds, including zero and all positive real numbers, though none of these bounds belong to R^- directly. For example, zero is excluded from R^-, and an infinite amount of real numbers exist between zero and any negative real number. Moreover, R^- is devoid of lower bounds due to its indefinite extension below -∞.

Additionally, there are sets equipped with both upper and lower bounds.

Such sets are bounded sets, confined both below and above.

Example of a set with both upper and lower bounds. The real numbers ranging between -1 and +1 compose a subset within the real numbers R. This subset boasts an infinite number of lower bounds within the interval (-∞, -1) and similarly countless upper bounds within the range (1,+∞).

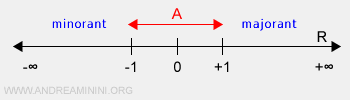
Lastly, certain sets exist without either upper or lower bounds.

Example of a boundless set. The empty set is an improper subset of every other universal set, devoid of both upper and lower bounds. Likewise, any set unlimited both below and above, such as the real numbers R, is an improper subset of itself, thereby lacking any bounds.

And the list goes on.