Relations Defined on a Set

A relation is said to be defined on a set when it links elements of a set A to other elements within the same set A.

In this context, the domain and codomain are one and the same.

Such a relation is a subset of the Cartesian product A × A.

A Practical Example

Let’s consider the finite set A:

$$ A = \{ 2,3,4,5,6,7,8,9 \} $$

The Cartesian product of A with itself, A × A, is given by:

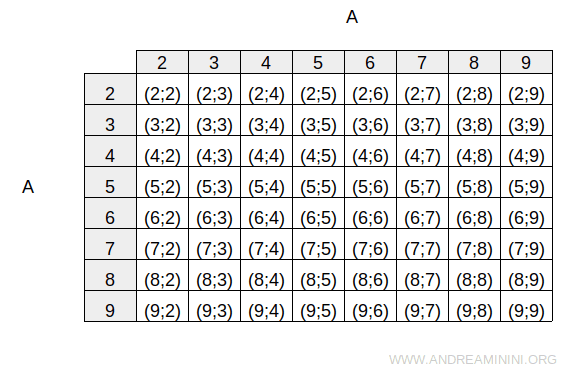
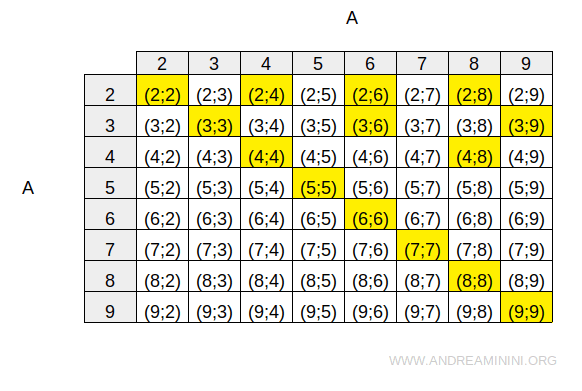
We define a relation R on A that associates each element with its multiples:

$$ R = \{ (2;2) , (2;4),(2;6),(2;8),(3;3),(3;6),(3;9)\\ \ \ \ \ \ \ \ \ \ \ \ \ (4;4) , (4;8),(5;5),(6;6),(7;7),(8;8),(9;9) \} $$

This relation is a subset of the Cartesian product A × A.

Here is how the relation is displayed using a two-way table:

The arrow diagram (or mapping diagram) of this relation is shown below:

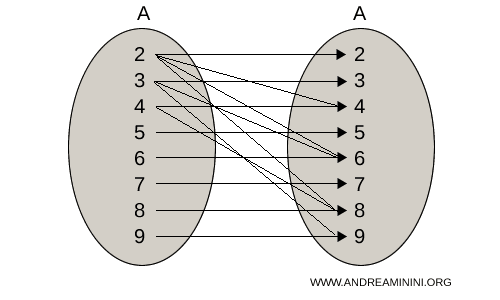
In this case, the same set A serves as both the domain and codomain.

Here is the corresponding Cartesian diagram of the relation:

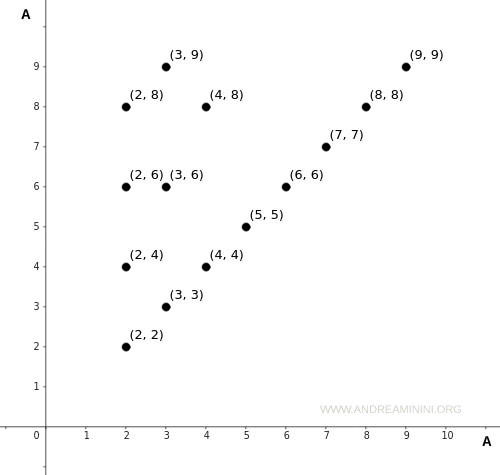
As shown, the set A is placed along both the horizontal (x-axis) and vertical (y-axis) axes.

Note. Relations defined on a set can be represented more intuitively using a graph. Simply represent each element of A as a node, without enclosing them in a boundary, and connect related elements with directed edges called arcs. If an element is related to itself - such as (2;2) - this forms a special type of edge called a loop. For relations defined on a set, graph-based representations are often more concise, readable, and visually effective.

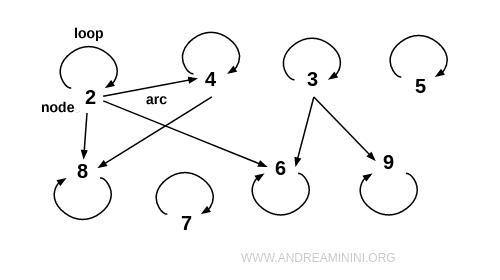
Types of Relations Defined on a Set

There are several important types of relations that can be defined on a set:

• Reflexive Relation
  A relation R on a set A is reflexive if every element a ∈ A is related to itself. $$ \forall \ a \in A \Rightarrow \ aRa $$
• Irreflexive Relation
  A relation R on a set A is irreflexive if no element a ∈ A is related to itself. $$ \forall \ a \ \in A \ \Rightarrow a \require{cancel} \cancel{R} a $$
• Symmetric Relation
  A relation R on a set A is symmetric if, for all a, b ∈ A, whenever a is related to b, then b is also related to a. $$ aRb \ \Leftrightarrow \ bRa $$
• Asymmetric Relation
  A relation R on a set A is asymmetric if, for all a, b ∈ A, whenever a is related to b, then b is not related to a. $$ aRb \Rightarrow b \require{cancel} \cancel{R} a $$
• Antisymmetric Relation
  A relation R on a set A is antisymmetric if, for all distinct elements a, b ∈ A (with a ≠ b), whenever a is related to b, then b is not related to a. $$ aRb , \ a \ne b \Rightarrow b \require{cancel} \cancel{R} a $$

  What’s the difference between asymmetric and antisymmetric? An antisymmetric relation allows two elements to be mutually related only if they are equal. In other words, if both aRb and bRa hold, then a must be equal to b. $$ aRb , \ a \ne b \Rightarrow b \require{cancel} \cancel{R} a $$ In contrast, an asymmetric relation prohibits any mutual relation - whether the elements are equal or not. $$ aRb \Rightarrow b \require{cancel} \cancel{R} a $$ So, asymmetry rules out reciprocal pairs altogether, while antisymmetry allows them only when the elements are identical.

• Transitive Relation
  A relation R on a set A is transitive if, for all a, b, c ∈ A, whenever a is related to b and b is related to c, then a is also related to c. $$ aRb , \ bRc \Rightarrow aRc $$

And so on.