Intersection of Open Sets in Quotient Topology

In quotient topology, the preimage of the finite intersection of a collection of open sets $ U_i $ is equal to the intersection of the preimages of those sets, which forms an open set in the original topology of X. $$ p^{-1}( \bigcap U_i ) = \bigcap p^{-1}(U_i) $$ Thus, a finite intersection of open sets is itself an open set in the quotient topology.

A Practical Example

Consider the common quotient space \( A = \mathbb{R}/\mathbb{Z} \), which we can visualize as a circle.

In this setting, the original space is the real numbers $ \mathbb{R} $, and the quotient map \( p: \mathbb{R} \to \mathbb{R}/\mathbb{Z} \) sends each real number to its fractional part.

The quotient space itself is represented by the interval [0,1).

For instance, the numbers 0.3, 1.3, and 2.3 all map to 0.3 on the circle.

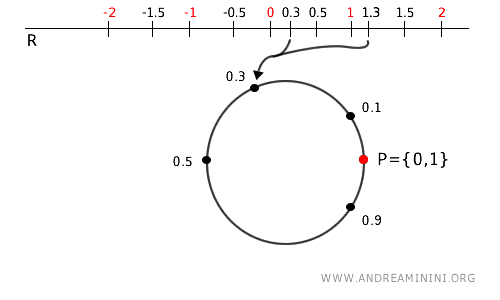
Now, let’s take two open sets on the circle \( A \):

$$ U_1 = (0.1, 0.5) $$

$$ U_2 = (0.3, 0.7) $$

These intervals are open in the quotient topology \( \mathbb{R}/\mathbb{Z} \).

Let’s now find their intersection:

$$ U_1 \cap U_2 = (0.3, 0.5) $$

The intersection is clearly open on the circle, as it’s simply another open interval.

In \( \mathbb{R} \), the preimages of these sets under the map \( p \) consist of an infinite union of open intervals repeated along the real line.

The preimage of \( U_1 \) is:

$$ p^{-1}(U_1) = (0.1, 0.5) \cup (1.1, 1.5) \cup (2.1, 2.5) \cup \dots $$

Similarly, the preimage of \( U_2 \) is:

$$ p^{-1}(U_2) = (0.3, 0.7) \cup (1.3, 1.7) \cup (2.3, 2.7) \cup \dots $$

Now, let’s compute the preimage of their intersection.

The preimage of \( U_1 \cap U_2 \) in \( \mathbb{R} \) is the intersection of the preimages of \( U_1 \) and \( U_2 \):

$$ p^{-1}(U_1 \cap U_2) = (0.3, 0.5) \cup (1.3, 1.5) \cup (2.3, 2.5) \cup \dots $$

This is a union of open intervals in the standard topology of \( \mathbb{R} \), meaning the preimage is open in \( \mathbb{R} \).

Since the preimage of the intersection is an open set in \( \mathbb{R} \), we can conclude that the intersection \( U_1 \cap U_2 \) is open in the quotient topology \( \mathbb{R}/\mathbb{Z} \).

Therefore, the finite intersection of open sets in the circle is open, as expected.

And so forth.