Union of Open Sets in Quotient Topology

Given a collection of open sets $ U_i $ in the quotient topology Q, the preimage of their union is the union of their preimages, which consists of open sets in the original topology X. $$ p^{-1}( \bigcup U_i ) = \bigcup{ p^{-1}(U_i) } $$ Therefore, the union of open sets is also open in the quotient topology.

An Illustrative Example

Let's consider the set of real numbers $ \mathbb{R} $ and define a quotient topology using the map $ p: \mathbb{R} \to \mathbb{R}/\mathbb{Z} $, which sends every real number $ x \in \mathbb{R} $ to its equivalent modulo 1.

In simpler terms, the image of each real number is just its fractional part.

For example, under the map $ p $, the numbers 0.3, 1.3, 2.3, etc., all map to 0.3 in the quotient topology.

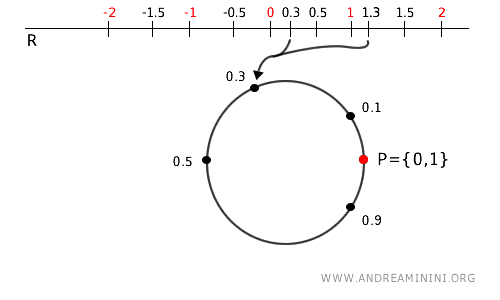
example

Thus, the quotient space Q is essentially a circle made up of real numbers ranging from 0 (inclusive) to 1 (exclusive), or [0,1).

Now, let’s consider a collection of open sets in the interval $ Q = \mathbb{R}/\mathbb{Z} $. For instance:

$ U_1 = (0.1, 0.4) $
$ U_2 = (0.6, 0.8) $

These are open sets in the quotient space $ Q $, which corresponds to the circle.

Next, I want to investigate what happens when we take the union of these two open sets in the quotient topology.

The preimage of $ U_1 $ under the map $ p $ is the union of all the corresponding open intervals: \[ p^{-1}(U_1) = (0.1, 0.4) \cup (1.1, 1.4) \cup (2.1, 2.4) \cup \dots \]
Similarly, the preimage of $ U_2 $ under the map $ p $ is the union of all the corresponding open intervals: \[ p^{-1}(U_2) = (0.6, 0.8) \cup (1.6, 1.8) \cup (2.6, 2.8) \cup \dots \]

The union of the sets $ U_1 $ and $ U_2 $ in the interval [0,1) of the quotient space $ Q $ is:

$$ U_1 \cup U_2 = (0.1, 0.4) \cup (0.6, 0.8) $$

The preimage of this union is equal to the union of the preimages:

$$ p^{-1}(U_1 \cup U_2) = p^{-1}(U_1) \cup p^{-1}(U_2) $$

This simplifies to:

$$ p^{-1}(U_1 \cup U_2) = (0.1, 0.4) \cup (0.6, 0.8) \cup (1.1, 1.4) \cup (1.6, 1.8) \cup \dots $$

The union of these preimages is a collection of open intervals in $ \mathbb{R} $, which means it is open in $ \mathbb{R} $.

Therefore, the union of the open sets $ U_1 \cup U_2 $ is also open in the quotient topology on $ A = \mathbb{R}/\mathbb{Z} $.

And so on.