Polygonal Chains

In geometry, a polygonal chain (or polygonal line) is a sequence of line segments, each joined end-to-end to create a chain or network. The segments are commonly referred to as sides, while their endpoints are known as vertices.

Each vertex in a polygonal line can connect to no more than two segments.

Polygonal chains can be open, closed, or intersecting.

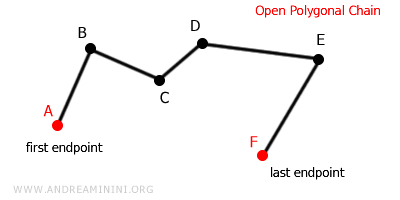
• Open Polygonal Chains
  In open polygonal chains, the last endpoint does not connect back to the first endpoint.
  
• Closed Polygonal Chains
  In closed polygonal chains, the last link in the chain connects back to the first endpoint.
  
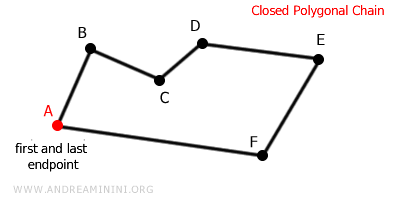
  Closed polygonal chains form a shape known as a polygon, which can take many forms. These can be regular, where all sides and angles are equal, or irregular.
• Intersecting Polygonal Chains
  In intersecting polygonal chains, at least two non-consecutive sides cross each other.
  

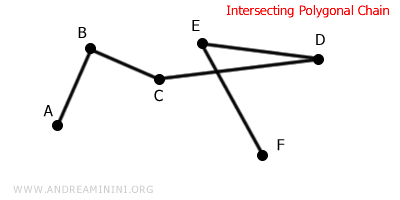
Practical Applications of Polygonal Chains. In topography, polygonal chains consist of precisely measured points used to determine the relative positions of points on the Earth's surface. This technique is essential for mapping and land surveying. Polygonal chains are also widely used in computer graphics for modeling three-dimensional shapes. For example, in video games and animations, 3D objects are often represented as a network of polygons, with each polygon representing a portion of the object's surface. This method is known as polygonal modeling.

And so on.