Cartesian Plane

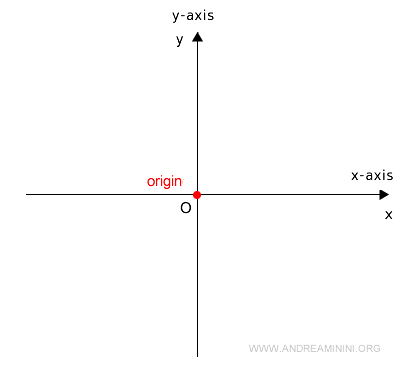
The Cartesian plane is composed of two perpendicular lines, or axes, that intersect at a right angle:

• A horizontal axis known as the x-axis, represented by the letter x.
• A vertical axis known as the y-axis, represented by the letter y.

The point where the x-axis and y-axis meet is called the origin (O), which marks the zero point for both x and y.

Note: The equations for the Cartesian axes are derived by setting y=0 for the x-axis and x=0 for the y-axis. The equation of the x-axis is a specific case of the line equation y=mx+q, where m=0 and q=0. Conversely, the y-axis cannot be expressed using the line equation y=mx+q.

Both Cartesian axes have a defined direction and are numbered accordingly.

Points to the right of the origin on the x-axis are positive, while those to the left are negative.

Points above the origin on the y-axis are positive, while those below are negative.

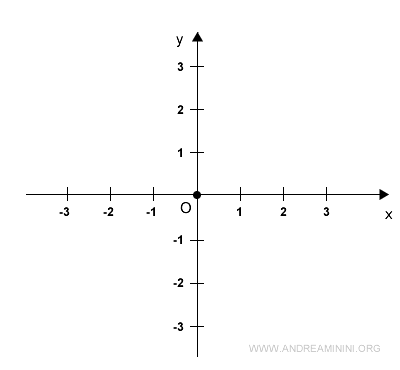
Each axis is associated with a specific unit of measurement, which may be the same or different for each axis.

Note: The Cartesian system is called monometric if both axes use the same unit of measurement. It is called dimetric if each axis uses a different unit of measurement.

Every point on the plane is identified by an ordered pair of numbers (x,y), known as Cartesian coordinates.

The first number in the pair corresponds to a value on the x-axis, while the second number corresponds to a value on the y-axis.

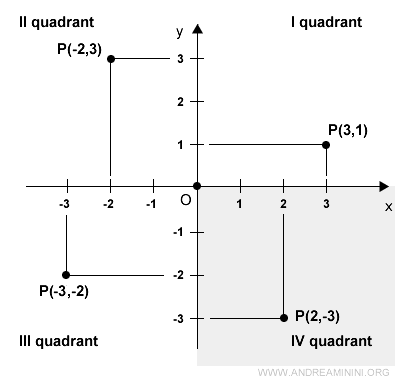
For example, the point P(3,1) is located at x=3 and y=1.

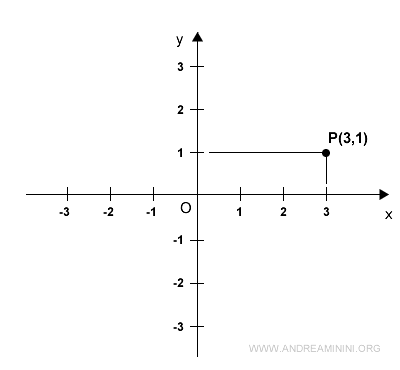
The origin, O, is located at the coordinates (0,0), where x=0 and y=0.

There is a one-to-one correspondence between the points on the plane and their Cartesian coordinates (x;y).

• Each point P on the plane corresponds to one and only one ordered pair (x;y) of real numbers.
• Each ordered pair (x;y) of real numbers corresponds to one and only one point P on the plane.

The Quadrants of the Cartesian Plane

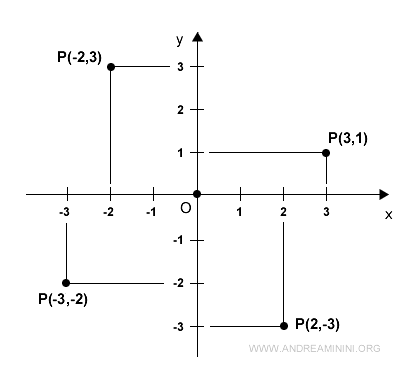
The Cartesian plane is divided into four quadrants, numbered counterclockwise.

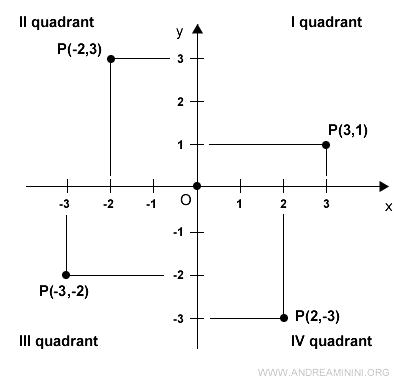
In the first quadrant, both x and y are positive.

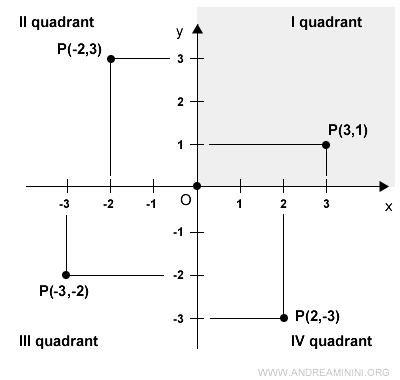
In the second quadrant, x is negative while y is positive.

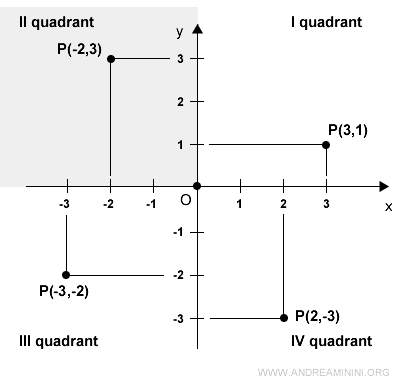
In the third quadrant, both x and y are negative.

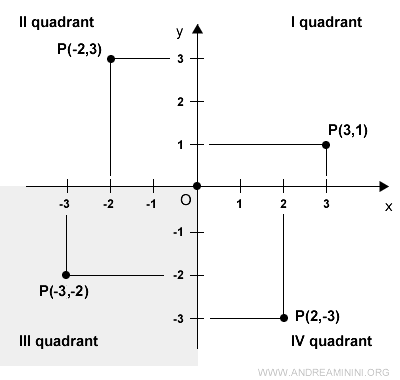
In the fourth quadrant, x is positive while y is negative.

And so on.