Geometric Quantities

Classes of geometric quantities are fundamental concepts in both mathematics and geometry.

These classes encompass various measurements and properties of shapes and figures, such as length, area, volume, angles, and more.

Examples of Geometric Quantity Classes

Some of the most common geometric quantities include:

• Length
  Length refers to the measurement of a straight line from one point to another. It is the most basic dimension, measured in units such as meters, centimeters, inches, etc.
• Area
  Area measures the two-dimensional space within a figure, such as the area of a square or circle. It is expressed in square units like square meters, square centimeters, etc.
• Volume
  Volume measures the three-dimensional space occupied by an object, such as the volume of a sphere or a cube. It is measured in cubic units like cubic meters, cubic centimeters, etc.
• Angles
  Angles measure the deviation between two lines that meet at a common point, known as the vertex. They are measured in degrees or radians.
• Surface Area
  Surface area is a general class that includes the area of two-dimensional figures and the total area covering the surface of a three-dimensional object.

These quantities are essential for studying and understanding the properties of geometric shapes in both pure mathematics and practical applications.

Homogeneous Geometric Quantities

Quantities are considered homogeneous when they belong to the same geometric class.

In other words, two quantities are homogeneous if they can be directly compared or combined because they share the same nature or dimension.

For instance, two or more lengths are homogeneous if they are measured in the same unit (such as meters, kilometers, inches, etc.), and therefore can be added or subtracted.

5 meters and 3 meters are homogeneous quantities.

Similarly, areas are homogeneous if they are measured in the same unit (such as square meters, hectares, acres, etc.).

Two volumes are homogeneous if expressed in the same unit of measurement (such as liters, cubic meters, etc.).

Angles are homogeneous when measured in the same unit, such as degrees or radians.

Non-homogeneous quantities cannot be directly combined. For example, it doesn't make sense to add a length to an area or a volume to an angle because they belong to different quantity classes. However, you can often convert quantities into compatible units to make them homogeneous if necessary.

Multiples and Submultiples of a Quantity

A quantity A is called a multiple of a homogeneous quantity B if it is n times the quantity B. $$ A = n \cdot B $$ Where n is a natural number greater than or equal to zero (n≥0).

When we talk about a multiple of quantity A by a natural number n, we refer to a quantity B that is homogeneous to A. This means B and A are of the same type or nature (for example, both could be lengths, times, masses, etc.).

Here’s how A is defined in terms of B and n:

• If n is greater than or equal to 1
  In this case, A is the sum of n quantities equal to B.

  For example, consider two segments AB and CD. They are homogeneous quantities because they are both lengths. If segment CD is three times (n=3) the length of segment AB, and segment AB is 2 meters long, then segment CD is 6 meters long and is a multiple of segment AB by a natural number n=3. $$ \overline{CD} = 3 \cdot \overline{AB} $$
  /geometry/commensurable-and-incommensurable-quantities

• If n is equal to 1
  In this case, A is simply equal to B. This is straightforward since adding a quantity to itself just once results in the same quantity. $$ A=B $$
• If n is equal to 0
  In this case, A is the null quantity, or zero. Practically speaking, if you don’t multiply a quantity by any factor (zero times), the result is a null quantity. $$ A= 0 \cdot B = 0 $$

To define a submultiple, you just reverse the relationship of a multiple.

If quantity A is a multiple of B, then B is a submultiple of A. $$ B = \frac{1}{n} \cdot A $$ Where n is always a natural number greater than zero (n>0).

In other words, quantity B is a fraction or a part of A.

We avoid considering the case n=0 because it would result in a division by zero, an impossible mathematical operation.

For example, if segment CD is a multiple of AB by a natural number n=3, then segment AB is a submultiple of CD by a fraction of 1/3. $$ \overline{AB} = \frac{1}{3} \cdot \overline{CD} $$
/geometry/commensurable-and-incommensurable-quantities

Additional Notes

Here are some observations and additional notes on classes of geometric quantities:

• Are geometric classes groups?
  Geometric classes are not groups in the algebraic sense because they are not defined by an operation that satisfies the properties of groups.

  Geometric classes organize and categorize shapes and figures based on shared properties, whereas groups are algebraic structures that define a specific way to combine elements of a set.

• The Eudoxus-Archimedes Postulate
  This postulate states that if one quantity is smaller than another, it is always possible to add enough copies of the smaller quantity to exceed the larger one.
  
  

  Note. Of course, both quantities must be non-zero. If the smaller quantity were zero, all its multiples would also be zero, so no multiple could ever exceed the larger quantity.

• Commensurable and Incommensurable Geometric Quantities
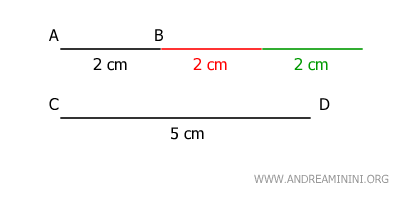
  Two homogeneous geometric quantities are commensurable if there exists a rational number m/n that relates them. Conversely, if no such number exists, the quantities are incommensurable.

  Example. The lengths of segments AB and CD are commensurable quantities
  
  because there exists a rational number m/n that relates them. $$ \overline{AB} = \frac{2}{5} \cdot \overline{CD} $$ Where m and n are two integers.

And so on.