Directly Proportional Quantities

Directly proportional quantities are two related quantities that share a linear relationship.

This means that as one quantity increases, the other increases in direct proportion, and the same applies if one decreases.

Mathematically, two quantities A and B are directly proportional if there is a constant k such that:

$$ A = k \cdot B $$

The constant k is known as the proportionality constant or proportionality ratio.

$$ k = \frac{A}{B} $$

In simpler terms, there is a one-to-one correspondence between these two quantities.

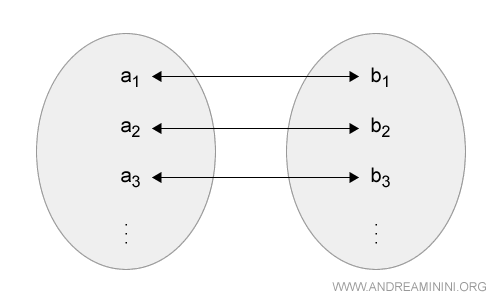
If you take any two elements a₁ and a₂ from the set of quantity A, their ratio will equal the ratio of the corresponding elements b₁ and b₂ in the set of quantity B.

$$ \frac{a_1}{a_2 }= \frac{b_1}{b_2} $$

This can be expressed as: "a₁ is to a₂ as b₁ is to b₂."

$$ a_1 : a_2 = b_1 : b_2 $$

Of course, this is only valid if a₂ and b₂ are non-zero, as dividing by zero is undefined.

For example, if A is directly proportional to B with a proportionality constant of k=2, then when B is 3, A will be 6; and when B is 5, A will be 10.

For instance, consider two elements from A, 1 and 4, whose ratio is 0.25: $$ \frac{1}{4} = 0.25 $$ The corresponding elements from B are 2 and 8, and their ratio is also 0.25: $$ \frac{2}{8} = 0.25 $$

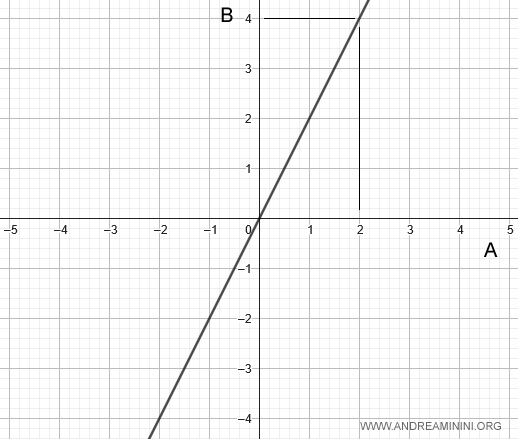
On a graph, directly proportional quantities are represented by a straight line that passes through the origin.

The Direct Proportionality Theorem

These two conditions ensure a one-to-one correspondence between quantities A and B.