Contiguous Quantitie
Two sets of quantities, A and B, are referred to as contiguous quantities if:
- Every quantity in set A is smaller than every quantity in set B
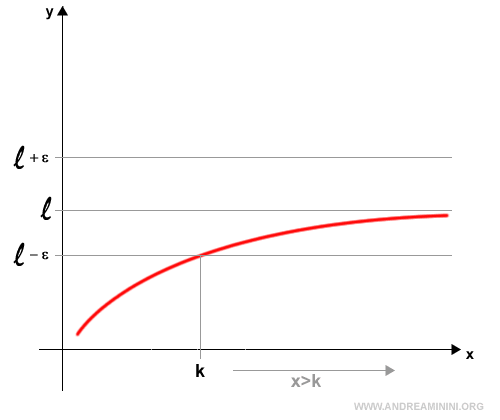
- No matter how small a homogeneous quantity ε is chosen, it is possible to find a quantity from set A and a quantity from set B such that the difference between them is less than epsilon. $$ B-A < \epsilon $$
In other words, there exists a value called the separator element between the two contiguous sets, which is no smaller than any quantity in set A and no larger than any quantity in set B.
Essentially, this separator element can be thought of as a boundary or limit between the two sets of quantities.
Note: The concept of contiguous quantities and a separator element plays a fundamental role in limit calculations, infinitesimal calculus, and mathematical analysis.
For example, when defining the limit of a function at a point, we are implicitly dealing with contiguous quantities: the values of the function get arbitrarily close to a certain limiting value (the separator element) but never actually reach it.
This way of thinking about mathematical quantities is closely connected to the continuity postulate, set theory, and the work of Cantor.
It provides a conceptual framework for dealing with infinity and continuity in mathematics, allowing for a more rigorous and formal exploration of ideas like convergence and continuity.
And so on.
