Inversely Proportional Quantities

Two quantities, A and B, are inversely proportional if, as one increases, the other decreases in such a way that the product of the two remains constant. $$k = A \cdot B$$

Another way to express this relationship is through the formula: A = k/B, where k is a constant. If B increases, A must decrease to keep k unchanged, and vice versa.

$$A = \frac{k}{B}$$

In other words, the ratio of any two elements a₁ and a₂ from set A is equal to the reciprocal of the corresponding elements b₁ and b₂ from set B.

$$\frac{a_1}{a_2} = \frac{b_2}{b_1}$$

This can also be expressed as "a₁ is to a₂ as b₂ is to b₁".

$$a_1 : a_2 = b_2 : b_1$$

It’s important to note that a₂ and b₁ must not be zero to avoid the issue of division by zero.

For instance, if A is inversely proportional to B and their product A·B is always equal to k=1, then when A is 2, B will be 0.5; when A is 4, B will be 0.25. In every scenario, the product remains constant at 1.

As another example, consider two elements from A, 4 and 2, whose ratio is 2: $$\frac{4}{2} = 2$$ The corresponding elements from set B are 0.25 and 0.50, and their ratio is the reciprocal of 2, which is 1/2: $$\frac{0.25}{0.5} = \frac{ \frac{1}{4} }{ \frac{1}{2} } = \frac{1}{4} \cdot \frac{2}{1} = \frac{2}{4} = \frac{1}{2}$$

In a graph, inversely proportional quantities are depicted by a rectangular hyperbola with the transverse axis along the bisector. This reflects how, as A increases and B decreases, the product AB remains constant.

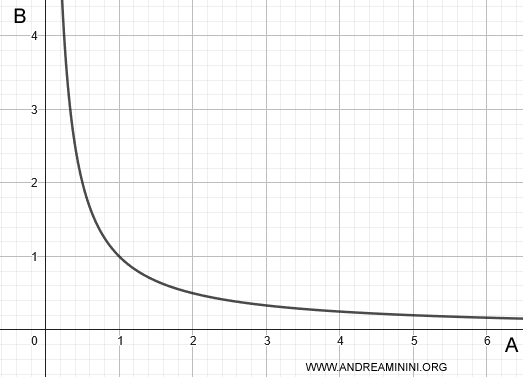
Note: This concept is especially useful in physics. For example, in Coulomb's law, the force between two electric charges is inversely proportional to the square of the distance between them.

A Practical Example

Consider the relationship between speed and the time required to travel a fixed distance.

$$\text{time} = \text{distance} / \text{speed}$$

If the speed increases, the time needed to cover the distance decreases, but the product of speed and time, which equals the distance, remains constant.

$$\text{speed} \cdot \text{time} = \text{distance}$$

For example, let's say you want to travel a distance of 100 km.

If you travel at a speed of 50 km/h, it will take you 2 hours to cover the distance.

$$\text{Time} = \text{100 km} / \text{50 km/h} = \text{2 h}$$

If you double the speed to 100 km/h, the time required to cover the same distance is halved to 1 hour.

$$\text{Time} = \text{100 km} / \text{100 km/h} = \text{1 h}$$

In this example, speed (V) and time (T) are inversely proportional, with the distance traveled remaining constant at 100 km.

When the speed doubles, the time is halved. In both cases, the product of V and T equals 100 km.

$$\text{50 km/h} \cdot \text{2 hours} = \text{100 km}$$

$$\text{100 km/h} \cdot \text{1 hour} = \text{100 km}$$

This illustrates how, by keeping the distance constant, increasing the speed proportionately decreases the time required to travel it.

And so on.