Continuous Quantities

The postulate of continuity of quantities formalizes the intuitive idea that mathematical quantities can be divided into infinitely smaller parts without limit.

This concept is essential for understanding the structure of real numbers and the development of mathematical analysis.

It's often linked to Georg Cantor and his pioneering work in set theory and the foundations of modern mathematics.

Note: In more technical terms, the postulate of continuity asserts that any quantity can be represented as a collection of indivisible units, which can be mapped one-to-one with the integers. Cantor used this principle to lay the groundwork for set theory and to delve into concepts like cardinality and the construction of real numbers.

A crucial aspect of this postulate is the notion of infinitely divisible quantities, which plays a fundamental role in infinitesimal calculus.

For instance, when considering the length of a segment AB, the postulate of continuity suggests that this segment can be divided into smaller and smaller parts indefinitely, without ever reaching an "indivisible smallest part."

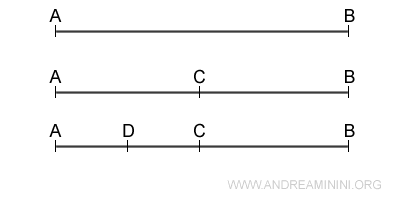
This ability to divide a segment (or any quantity) into ever-smaller parts without encountering an indivisible limit allows for precise handling of concepts such as limits, derivatives, and integrals.

Thus, Cantor's postulate of continuity was pivotal in the development of modern analysis, profoundly shaping the direction and nature of mathematics in the 20th century.

It led to the realization that real numbers can be understood as a continuum, meaning they are infinitely divisible.

Example: Given any two distinct real numbers a<b, there will always be a real number c such that a<c<b. For instance, between 2 and 3, there are infinitely many intermediate real numbers (e.g., 2.5, 2.49, 2.77, ...). Likewise, between 2 and 2.5, there are also infinitely many intermediate real numbers. And so forth.

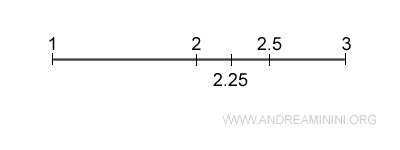
This concept is fundamental for understanding the density of real numbers and, more broadly, any numerical set.

This understanding has helped resolve paradoxes and problems related to infinity and continuity in mathematical functions.

For example, Zeno's paradox illustrates the challenges faced by ancient Greek mathematicians in conceptualizing infinity and infinite division.

Zeno argued that a hare (or Achilles) could never overtake a tortoise if the tortoise had a head start, because the hare would first need to reach the point where the tortoise began, by which time the tortoise would have moved further ahead.

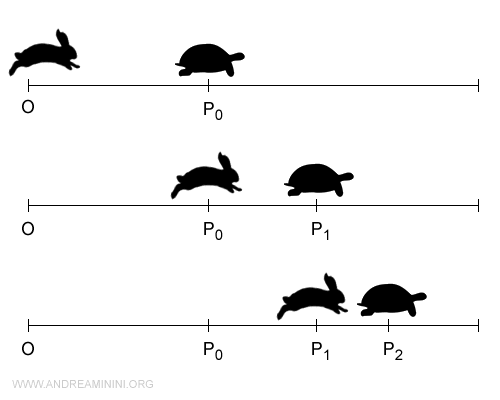
The postulate of continuity also had significant implications for the development of infinitesimal calculus.

The very notions of limits and continuity hinge on the idea that it is possible to approach a value arbitrarily closely without necessarily reaching it.

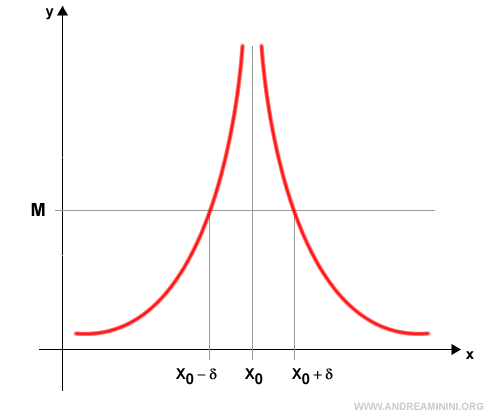
This concept is particularly important in calculating derivatives and integrals, where one works with quantities that are infinitesimally small.

And so on.