Proportional Quantities

Two pairs of homogeneous quantities, A, B and C, D, where B and D are non-zero, are called proportional quantities if the ratios A/B and C/D are equal, which can also be expressed as $$ \frac{A}{B} = \frac{C}{D} $$ or $$ A:B = C:D $$.

This means that A relates to B in the same way that C relates to D. In simpler terms, the proportion shows that the ratio of A to B is identical to the ratio of C to D.

$$ \frac{A}{B} = \frac{C}{D} $$

This is read as "A is to B as C is to D."

A proportion is an equivalence relationship and holds true only when B and D are non-zero, as division by zero is undefined in mathematics.

Similar to numerical proportions, in a proportion between quantities, A and D are known as the extremes, while B and C are known as the means.

The numerators of the ratios (A and C) are called the antecedents, while the denominators (B and D) are called the consequents.

Note: It is not necessary for all quantities to be homogeneous; it is sufficient that the numerators are homogeneous with each other and that the denominators are homogeneous with each other. Therefore, a proportion can also be formed between two non-homogeneous quantities.

The concept of proportion between quantities is highly useful in mathematics, geometry, and physics as it enables the solving of various types of problems.

A Practical Example

Consider a scenario where a "blue" car has traveled a distance of 100 km in 2 hours, while another "red" car has covered an unknown distance \( D \) in 4 hours.

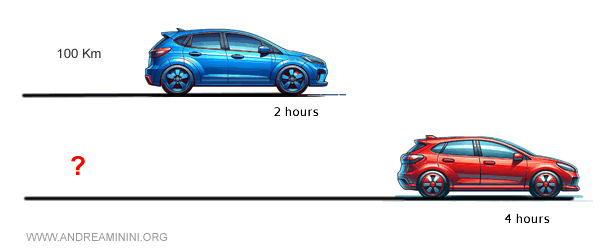
We want to determine the distance \( D \) traveled by the red car, assuming both cars maintained the same constant speed.

The quantities we are comparing are the distance traveled and the time taken. We can set up the proportion as follows:

\[ \frac{\text{Distance}_1}{\text{Time}_1} = \frac{\text{Distance}_2}{\text{Time}_2} \]

In this case, we already know all the information for the blue car (distance and time) but only the time for the red car.

\[ \frac{100\, \text{km}}{2\, \text{hours}} = \frac{D\, \text{km}}{4\, \text{hours}} \]

To find the distance \( D \) traveled by the red car, we need to solve the proportion:

\[ \frac{100}{2} = \frac{D}{4} \]

\[ 50 = \frac{D}{4} \]

\[ D = 50 \times 4 \]

\[ D = 200\, \text{km} \]

Thus, the red car traveled 200 km in 4 hours, assuming it maintained the same speed as the blue car.

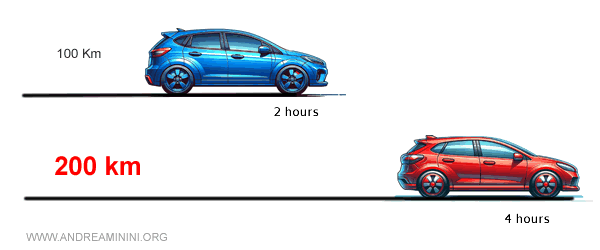
This is the solution to the problem.

\[ \frac{100\, \text{km}}{2\, \text{hours}} = \frac{200\,  \text{km}}{4\, \text{hours}} \]

The two pairs of quantities are proportional because the ratio is the same.

$$ 50 \ \text{km/h} = 50 \ \text{km/h} $$

Both cars are traveling at 50 kilometers per hour.

Note: This example illustrates how proportions can be used to solve practical problems, particularly when homogeneous quantities are involved in both the antecedents and the consequents (in this case, distance and time), and a constant relationship (constant speed) is assumed between them.

Properties of Proportions Between Quantities

The properties of proportions between quantities are mathematical principles that describe the consistent relationship between two or more quantities. Some of the most significant properties of proportions include:

• Fundamental Property
  This property states that the product of the means equals the product of the extremes in a proportion.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow ad = bc $$

• Inversion Property
  This property indicates that the terms of a proportion can be reversed.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{b}{a} = \frac{d}{c} $$

• Alternation Property
  This property allows the means or the extremes of a proportion to be swapped.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a}{c} = \frac{b}{d} $$

• Composition Property
  This property suggests that the sum of the consequents to their respective antecedents remains proportional.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a+b}{b} = \frac{c+d}{d} $$

• Decomposition Property
  This is the opposite of the composition property.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a-b}{b} = \frac{c-d}{d} $$

• Addition and Subtraction Property
  This property indicates that the proportion remains unchanged if the same number \( n \) is added to or subtracted from the antecedents and consequents of each proportion, as long as \( n \) does not result in a zero denominator.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow\frac{a+n}{b+n} = \frac{c+n}{d+n} $$ $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a-n}{b-n} = \frac{c-n}{d-n} $$

• Multiplication Property
  The proportion remains unchanged if both the antecedent and consequent terms of a proportion are multiplied by the same non-zero real number.
  

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a \cdot h}{b \cdot h} = \frac{c}{d} \ \ \ if \ \ \ h \ne 0 $$ $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a}{b} = \frac{c \cdot k}{d \cdot k} \ \ \ if \ \ \ k \ne 0 $$

• Chain of Equal Ratios Property
  If three pairs of homogeneous quantities form equal proportions, then the proportion between the sum of the antecedent terms and the sum of the consequent terms is equal to each of the original proportions.

  $$ \frac{a}{b} = \frac{c}{d} = \frac{e}{f}  \Longleftrightarrow \frac{a+c+e}{b+d+f}  = \frac{a}{b} $$

These properties are crucial for solving problems involving proportions in various fields.

Additional Remarks

Here are some additional remarks and notes on proportional quantities.

• Corollary
  If two pairs of homogeneous quantities A, B and C, D are proportional, then their measurements are also proportional. $$ \frac{A}{B} = \frac{C}{D} \Longleftrightarrow \frac{M(A)}{M(B)} = \frac{M(C)}{M(D)}  $$

  Proof: Knowing from the theorem of the ratio between homogeneous quantities that the ratio of the quantities A/B is equal to the ratio of their measurements M(A)/M(B), we deduce that if two ratios of homogeneous quantities are equal $ \frac{A}{B} = \frac{C}{D} $, then the ratios of their respective measurements must also be equal $ \frac{M(A)}{M(B)} = \frac{M(C)}{M(D)} $

• Continuous Proportions
  A proportion between homogeneous quantities is called continuous if the two means are equal: $$ A:X = X:D $$ where X is the mean proportional element.
• Theorem of the Fourth Proportional
  Given three non-zero homogeneous quantities A, B, and C, there exists a unique quantity D such that A:B=C:D $$ \frac{A}{B} = \frac{C}{D} $$

  Note: The fourth proportional is determined by the quantities A, B, and C as follows: $$ D= C \cdot \frac{B}{A} $$