Commensurable and Incommensurable Quantities

Commensurable quantities are homogeneous quantities that can be directly compared or measured in terms of one another, thanks to a common submultiple.

In other words, two quantities are commensurable if they can be expressed as multiples of the same unit of measurement.

Conversely, if this isn’t possible, the quantities are considered incommensurable.

For example, take the length and width of a room. If both are measured in meters, they can be directly compared because they’re expressed in the same unit of measurement. In this case, length and width are commensurable.

If two homogeneous quantities, A and B, are commensurable, they can be expressed using the same unit of measurement (U):

$$ A = m \cdot U $$

$$ B = n \cdot U $$

This means they can also be related to each other, indicating that there exists a rational number m/n that relates them:

$$ A = \frac{m}{n} \cdot B $$

Similarly, there’s a number n/m that relates them in the opposite way:

$$ B = \frac{n}{m} \cdot A $$

Here, m and n are two integers.

Thus, the ratios m/n and n/m are rational numbers.

Proof: Consider quantity A, $$ A = m \cdot U $$. Knowing that the unit of measurement can be expressed in relation to both quantities A and B, $$ U = \frac{1}{m} \cdot A = \frac{1}{n} \cdot B $$, by substituting U = (1/n) · B, we can relate quantities A and B through the ratio m/n. $$ A = m \cdot U = m \cdot ( \frac{1}{n} \cdot B ) = \frac{m}{n} \cdot B $$ Alternatively, they can be related through the ratio n/m: $$ B = n \cdot U = n \cdot ( \frac{1}{m} \cdot A ) = \frac{n}{m} \cdot A $$

So, commensurable quantities are those that can be measured relative to each other through a ratio expressed by a rational number.

For example:

$$ A = \frac{m}{n} \cdot B $$

In other words, two quantities are commensurable if the ratio between them is a number m/n that can be expressed as the quotient of two integers.

Note: This concept has ancient roots, dating back to the time of the ancient Greeks, particularly through the work of the Pythagoreans, who discovered that not all ratios of lengths, areas, or volumes can be expressed by rational numbers, leading to the discovery of irrational numbers.

A Practical Example

Let’s consider two segments, AB and CD, with lengths of 2 and 5 centimeters, respectively.

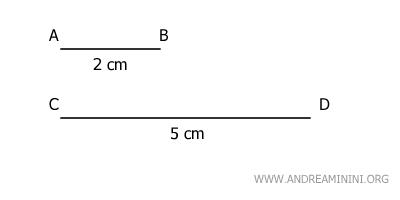
These are homogeneous quantities because they are comparable and expressed in the same unit of measurement.

We can think of segment AB as a multiple of one centimeter, specifically two times (n=2).

$$ \overline{AB} = 2 \cdot ( 1 \ cm ) $$

Similarly, segment CD can be thought of as a multiple of one centimeter, but five times (m=5).

$$ \overline{CD} = 5 \cdot ( 1 \ cm ) $$

Therefore, the lengths of segments AB and CD are commensurable because they share a common submultiple.

In other words, both AB and CD are multiples of 1 cm.

$$ 1 \ cm = \frac{1}{2} \cdot \overline{AB} $$

$$ 1 \ cm = \frac{1}{5} \cdot \overline{CD} $$

Here, 1 cm is the unit of measurement (U), or more precisely, the number 1 represents the measure of the unit of measurement (cm).

$$ U = 1 \ cm = \frac{1}{2} \cdot \overline{AB} = \frac{1}{5} \cdot \overline{CD} $$

This means that one quantity can be expressed in terms of the other.

If the unit of measurement is U=1 cm, segment AB becomes:

$$ \overline{AB} = 2 \cdot U $$

And knowing that U = (1/5) · CD:

$$ \overline{AB} = 2 \cdot ( \frac{1}{5} \cdot \overline{CD} ) $$

$$ \overline{AB} = \frac{2}{5} \cdot \overline{CD} $$

Thus, segment AB is 2/5 the length of segment CD.

Note: Similarly, we can show that segment CD is 5/2 the length of segment AB: $$ \overline{CD} = \frac{5}{2} \cdot \overline{AB} $$

Example 2

Even if two homogeneous quantities are expressed in the same unit of measurement, they aren’t necessarily commensurable.

For example, the length of the diagonal and the side of a square are two segments that share the same unit of measurement (e.g., meters). Are they commensurable or incommensurable?

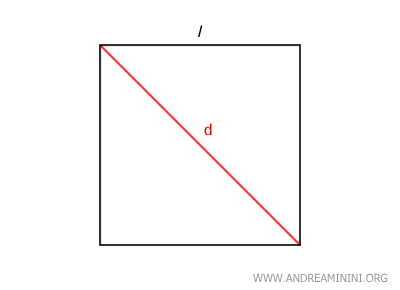
Even though they share the same unit of measurement, there is no rational number m/n that relates them.

From basic geometry, we know that the length of the diagonal (d) of a square is equal to the length of the side (l) of the square multiplied by the square root of 2.

$$ d = l \cdot \sqrt{2} $$

However, the square root of 2 is an irrational number, meaning it cannot be expressed as the ratio of two integers.

Therefore, in this case, we can say that the diagonal and the side of the square are incommensurable quantities when using rational numbers.

Observations

Some thoughts on the commensurability of quantities:

• Two incommensurable homogeneous quantities can be compared using real numbers
  The fact that two homogeneous quantities are incommensurable doesn’t mean they can’t be measured or compared with each other. However, instead of being compared through a rational number m/n, they’re compared through a real (or irrational) number α relative to the same unit of measurement. $$ A = \alpha \cdot B \ \ \ \ \alpha \in $$

  Example: The diagonal (d) of a square has a length equal to the product of the length of the side and the irrational number √2: $$ d = l \cdot \sqrt{2}$$

• Commensurability in modern physics and mathematics
  In modern physics and mathematics, the commensurability of two quantities isn’t determined by whether their ratio is a rational or irrational number, but rather by their ability to be measured in terms of each other using a common measure. In this context, commensurability refers to the possibility of describing different physical quantities in terms of common units or mathematical relationships, facilitating their comparison and understanding within unified theories like relativity or quantum mechanics.
• Commensurability in theoretical physics
  In more complex contexts beyond elementary geometry, such as in theoretical physics, the concept of commensurability can be more nuanced.

  For example, in Einstein’s theory of relativity, concepts like time and space, traditionally viewed as separate, are treated as aspects of a single entity, spacetime. This unified approach allows time and space to be considered differently, where they can be related in ways previously unrecognized. Therefore, the idea of commensurability can be connected to how Einstein treated time and space not as separate and absolute entities, but as interconnected parts of a broader framework, where measurements of one can influence and be influenced by the other.

And so on.