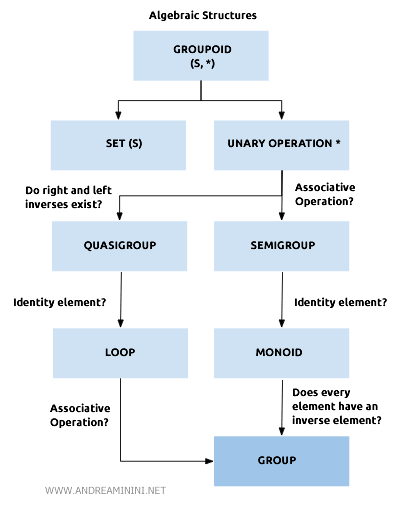
Groups
What is a Group?
- A group is an algebraic structure (G,*), which includes:
- a non-empty set (G≠Ø)
- a binary operation $$ *: G×G \rightarrow G $$ that satisfies three key properties:
- Associativity: $$ (a*b)*c = a*(b*c) $$
- Identity Element: There exists an identity element (e) in G such that $$ a*e=e*a=a \ \ \forall \ a \in G $$
- Inverses: Every element in G has an inverse $$ a*(a)^{-1}=(a)^{-1}*a= e \ \ \forall \ a \in G $$
In terms of abstract algebra, a group is a monoid (S,*) that also includes inverse elements for every member of set S.
The number of elements |G| in the set G determines the order of the group.
A group can be categorized based on the number of elements:
- Finite Group: The group has a finite number of elements.
- Infinite Group: The group has an infinite number of elements.
Groups are the cornerstone of group theory and abstract algebra, a relatively new area of mathematical study.
Practical Examples
Example 1: The set of integers (Z) with respect to addition (+)
- Addition is a binary operation internal to Z, and the sum of any two integers is another integer: $$ a+b = c \in Z \ \ \ \ \ \forall \ a,b \in Z $$
- It obeys the associative property: For any integers a, b, c ∈ Z, $$ (a + b) + c = a + (b + c) \ \ \ \ \ \forall \ a,b,c \in Z $$
- The identity element is 0 ∈ Z, meaning the sum of zero and any integer returns the same integer: $$ a+0=0+a=a \ \ \ \ \ \forall \ a \in Z $$
- Each integer has an additive inverse in Z. The sum of an integer and its negative is zero: $$ a+(-a)=(-a)+a=0 \ \ \ \ \ \forall \ a \in Z $$
Thus, (Z, +) forms an additive group.
Example 2: The set of integers (Z) with respect to multiplication (·) does not form a group because not all elements have a multiplicative inverse.
For instance, the multiplicative inverse of 2 is 1/2, which is not an integer: $$ 2 \cdot \frac{1}{2} = 1 $$
Note: In this case, the inverse element of multiplication is 1/2. While the set of integers Z with respect to multiplication meets several group properties (closed binary operation, associative property, identity element), it lacks inverses for all elements. Hence, Z does not form a group under multiplication. To view the full exercise.
Explore More about Groups:
- Group Theory
- Abelian Groups (Commutative)
Abelian Groups
A group is labeled abelian when it also adheres to the commutative property.
$$ (a*b)*c=a*(b*c) $$ $$ a*n=n*a=a $$ $$ a*a'=a'*a=n $$
Example
The set of rational numbers Q forms an abelian group under the addition operation (Q,+).
For any three integers (a,b,c), the associative rule is maintained:
$$ (a+b)+c=a+(b+c) $$
The identity element is zero:
$$ a+0 = 0+a = a $$
The inverse of a number is its negative counterpart.
$$ a + (-a) = (-a)+a= 0 $$
Its adherence to the commutative property confirms its status as an abelian group.
$$ a + b = b+a $$
Note: Excluding zero, the set of rational numbers also constitutes an abelian group under multiplication (Q,*), where 1 serves as the identity element and the reciprocal 1/a acts as the inverse element.
Non-Abelian Groups
A group is recognized as non-abelian if it does not comply with the commutative property.
Symmetric and dihedral groups are prime examples of non-abelian groups.
Example
The multiplication of two matrices violates the commutative property.
As a result, the matrix group under multiplication (M,*) qualifies as a non-abelian group.
$$ A \cdot B \ne B \cdot A $$
The product is derived through a row-by-column approach.
Note: In contrast, the matrix group (M,+) is abelian concerning addition. The sequence in which matrices are added in the sum of two matrices is irrelevant.
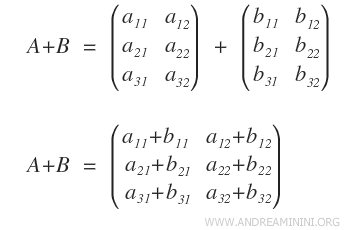
The Multiplication Table
If a group is composed of a finite number of elements, not too large, it can be represented using a table.
Each row and column is assigned an element of the finite group.
| a | b | ... | z | |
|---|---|---|---|---|
| a | a*a | a*b | ... | a*z |
| b | b*a | b*b | ... | b*z |
| ... | ||||
| z | z*a | z*b | ... | z*z |
The cells indicate the result of the binary operation.
Group Example
A group S is composed of the elements { 0,1,2,3,4,5,6,7} with respect to the addition operation + modulo 8.
What is addition modulo 8? It's a binary operation from clock arithmetic. In modular addition eight, any result greater than eight is equal to the modulo, i.e., the remainder. For example, 5+2=7, 6+2=0, 7+2=1, etc.
The composition table of the group (S,+8) is:
| a+b | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 |
| 3 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 |
| 4 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 |
| 5 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 |
| 6 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 |
| 7 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
It's a group because the binary operation is associative.
$$ 1+(2+3) = (1+2)+3=6 $$
An identity element (0) exists.
$$ 1+0=1 \\ 2+0=2 \\ \vdots $$
Every element has an inverse.
$$ 1+7=0 \\ 2+6=0 \\ 3+5=0 \\ 4+4=0 \\ 5+3=0 \\ 6+2=0 \\ 7+1 =0 $$
Group Order
The order of a finite group refers to its size, specifically the total count of its elements. Represented as $$ | G| $$, this measure is fundamental to understanding the group's structure.
Example
Consider the group S { 0,1,2,3,4,5,6,7}, operating under addition modulo 8. Here, the group's order is 8, indicating it comprises eight distinct elements.
$$ |S| = 8 $$
This means our group S includes eight unique members.
Element Order within a Group
An element's order, or its period, within a group (denoted as g in G,*), is identified by a positive integer h. This integer h is the smallest number of times the group's operation must be applied to g to return the group's identity element n: $$ g^h = n $$.
Should such an integer h not exist for g, it implies that g possesses an infinite period.
Conversely, if an integer h does exist for g, indicating a finite period n, then the subgroup generated by g, <g>, can be described as follows:
$$ <g> = \{ e, g, g^1, g^2, ... , g^{n-1} \} $$
In such scenarios, regardless of the differences between any two integers h and z (where h ≠ z), the equivalence $$ g^h \equiv g^z \mod n $$ always holds true.
Example
In the group S { 0,1,2,3,4,5,6,7} with respect to the addition operation + modulo 8, the order of the elements is as follows:
| Class | Order | Example |
|---|---|---|
| Class 0 | 1 | 01=0 |
| Class 1 | 8 | 18=0 |
| Class 2 | 4 | 24=2+2+2+2=0 |
| Class 3 | 8 | 38=3+3+3+3+3+3+3+3=0 |
| Class 4 | 2 | 42=4+4=0 |
| Class 5 | 8 | 58=5+5+5+5+5+5+5+5=0 |
| Class 6 | 4 | 64=6+6+6+6=0 |
| Class 7 | 8 | 78=7+7+7+7+7+7+7+7=0 |
The order of an element g is equal to the cardinality of the subgroup <g> generated by the element.
Example. Class 2 has an order of 4. The subgroup <2> generated by 2 is equal to $$ <2>=\{ 2, 4, 6, 0 \} $$ The subgroup <2> has 4 elements. Thus, the cardinality of the subgroup generated by 2 is equal to the order of 2, which is 4.
Exponentiation within Groups
Within group theory, the concept of exponentiation relates directly to the group's operation, distinct from its conventional mathematical usage.
Exponentiation of a group element, denoted as the nth power, represents the n-fold application of the group's operation on the element.
Example
Expressing g4 implies:
$$ g^4 = g \ast g \ast g \ast g $$
Note: The outcome hinges on the group's operation. For instance, with addition (+) as the operation, g4 equates to g+g+g+g. With multiplication (*), it results in g\ast g\ast g\ast g.
Negative exponentiation, such as g-4, denotes:
$$ g^{-4} = g^{-1} \ast g^{-1} \ast g^{-1} \ast g^{-1} $$
Zero exponentiation, by definition, returns the group's identity element:
$$ g^0 = e $$
Note: For groups under addition (G,+), g0=0; for groups under multiplication (G,*), g0=1.
Cyclic Groups
A group is termed cyclic if it contains an element g such that all elements of G can be generated by iteratively applying the group operation to g.
In essence, the subgroup generated by g encompasses the entire set.
Consider the addition-based modular arithmetic of eight as an example:
$$ G = (\{0,1,2,3,4,5,6,7\},+) $$
This forms a cyclic group as the element 1 acts as a generator, creating the whole set G through successive additions.
$$ <1> = \{1, 2, 3, 4, 5, 6, 7, 0\} = G $$
This illustrates that G is indeed a cyclic group of order 8.
Characteristics of Cyclic Groups
Key features of cyclic groups include their inherent abelian nature and the cyclic structure of every subgroup.
A noteworthy aspect is that the order of any subgroup must divide the group's order, and for each divisor of the group's order, there is precisely one corresponding subgroup of that order.
Infinite Cyclic Subgroups
A cyclic subgroup is considered infinite if its generating element has an infinite order, leading to distinct outcomes for differing powers, regardless of the integers chosen.
