Monoids

A monoid is a semigroup (S,*) that includes an identity element, e, which belongs to S. $$ \forall a \in S, e*a=a*e=a $$

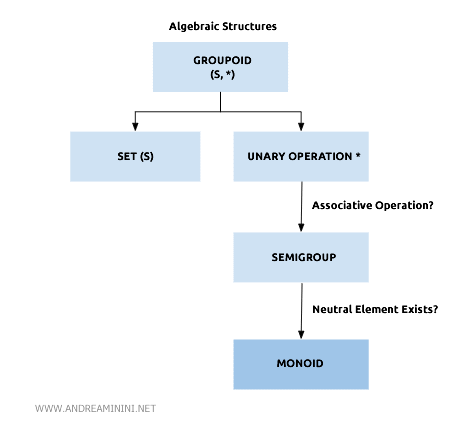
An algebraic structure (S,*) qualifies as a monoid if it acts as a groupoid, possesses all semigroup properties (such as associativity), and includes an identity element (e) for the operation * within set S.

Example

The semigroup (N,·) is composed of the set of natural numbers under the operation of multiplication (·).

This groupoid is considered a semigroup because multiplication is associative.

It also qualifies as a monoid because there is an identity element in the semigroup, which is the number 1.

Multiplying any number within the semigroup (N,·) by 1 results in the number itself.

$$ a \cdot 1 = 1 \cdot a = a $$

And so on.