Loop in abstract algebra
A loop is a type of quasigroup (S,*) that includes an identity element satisfying $$ a*x=a $$ and $$ x*a=a $$ for any element \(a\) in S.
Being a quasigroup, the algebraic structure (S,*) requires a right and left inverse for each pair of elements, \(a\) and \(b\), such that:
$$ a*d_x=b $$ $$ s_x*a=b $$
Unique to loops is the presence of a neutral element (e).
In a loop, for each pair of elements \(a\) and \(b\), there exists a unique element \(x\) in S serving as both the right and left inverse, where:
$$ a*x=b $$ $$ x*a=b $$
Loops fall within the broader category of groupoids.
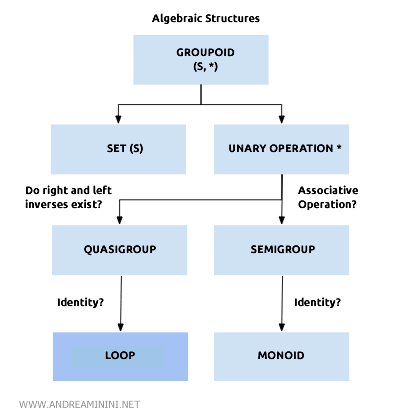
If the operation * in a loop also satisfies associativity, then the algebraic structure is termed an associative loop or group.
A Practical Example
The set of non-zero rational numbers Q-{0} under multiplication (·) forms a loop (Q-{0},·).
$$ (Q-\{ 0 \}, \cdot) $$
Examining the properties of this algebraic structure, we see:
Multiplication is a closed operation within the set of non-zero rational numbers Q-{0}, meaning:
$$ \forall a, b \in Q-\{ 0 \} \Longrightarrow a \cdot b \in Q-\{ 0 \} $$
Therefore, the structure (Q-{0},·) qualifies as a groupoid.
Example. Considering the integers a=4 and b=7, their product results in another rational number: $$ a \cdot b=4 \cdot 7=28 $$
For any pair of integers \(a\) and \(b\), there exists both a right and left inverse element.
Therefore, the structure (Z,·) is a quasigroup.
Example. Consider the integers a=4 and b=7. The inverse element \(x\) is \(7/4\): $$ a \cdot x = b $$ $$ 4 \cdot x = 7 $$ $$ x = \frac{7}{4} $$ and the same \(y=7/4\): $$ y \cdot a = b $$ $$ y \cdot 4 = 7 $$ $$ y = \frac{7}{4} $$ Note that the right and left inverses are the same.
In the algebraic structure (Q-{0},·), there exists an identity element, which is the number \(e=1\).
$$ \forall a \in Q-\{ 0 \} \Longrightarrow a \cdot 1 = 1 \cdot a = a $$
Thus, the structure (Q-{0},·) is a loop.
Note. Since multiplication is associative, the algebraic structure (Q-{0},·) qualifies as an associative loop, or a group. Consequently, all groups are loops, but the reverse is not true.
And so on.
