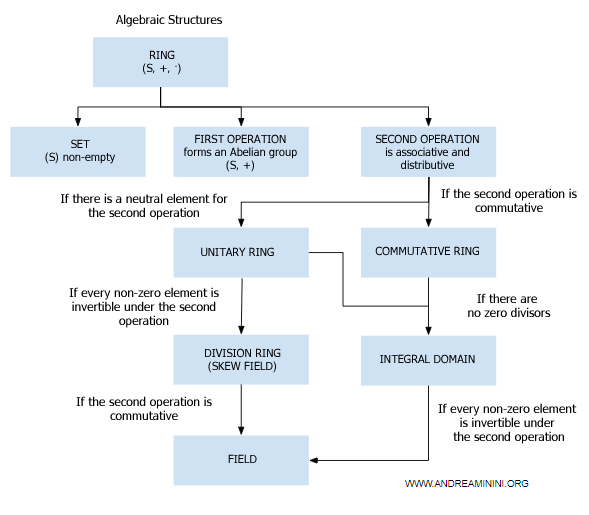
Division Ring (Skew Field)

In a division ring, there must be a multiplicative identity such that:

$$ a \cdot 1 = a \ \ \ \ \ \forall \ a \in R $$

Moreover, for each element other than the additive identity (zero), a multiplicative inverse must exist.

$$ a \cdot a^{-1} = 1 \ \ \ \ \ \forall \ a \ , \ a \ne 0 \ \ \in R $$

This means that in a division ring, the set S and the second operation (multiplication) form a group (S,·).

Note: Even though we use the terms "addition" and "multiplication," these operations could represent different ones in other contexts.

Importantly, the second operation (multiplication) does not need to be commutative.

If multiplication does satisfy the commutative property, the division ring is called a commutative division ring or a field.

A Practical Example

Consider the set of real numbers, R, with the operations of addition (+) and multiplication (·).

$$ (R, + , \cdot ) $$

To determine whether this algebraic structure is a division ring, let's check if both operations satisfy the necessary conditions.

The First Operation (+)

We begin by checking if addition forms an abelian group (R,+).

• Addition is closed under R, meaning that the sum of any two elements a, b ∈ R is also in R $$ \forall \ a,b \in R \ \ \ \ a+b \in R $$
• Addition is associative $$ \forall \ a,b,c \in R \ \ \ (a+b)+c = a+(b+c) $$
• Addition has an identity element $$ \forall \ a \in R \ \ \ a + 0 = 0 + a = a $$
• Every element of R has an additive inverse $$ \forall \ a \in R \ \ \ a + (-a) = (-a) + a = 0 $$

Thus, addition forms a group (R,+) with the real numbers.

Since addition is also commutative in R, this group (R,+) is an abelian group.

$$ \forall \ a,b \in R \ \ \ a+b = b+a $$

The first operation (+) satisfies all the required properties of a division ring.

The Second Operation (·)

Now, let's check if multiplication in R meets the requirements for a division ring.

• Multiplication is closed under R, meaning that the product of any two elements a, b ∈ R is also in R $$ \forall \ a,b \in R\ \ \ \ a \cdot b \in R $$
• Multiplication distributes over addition, both from the left and right $$ \forall \ a,b,c \in R \ \ \ \ a \cdot (b+c) = ab + ac $$ $$ \forall \ a,b,c \in R \ \ \ \ (a+b) \cdot c = ac + bc $$
• Multiplication is associative $$ \forall \ a,b,c \in R \ \ \ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$
• There is a multiplicative identity $$ \forall \ a \in R \ \ \ a \cdot 1 = 1 \cdot a = a $$
• Every non-zero element in R has a multiplicative inverse $$ \forall \ a \in R \ , \ a \ne 0 \ \ \ a \cdot a^{-1} = a^{-1} \cdot a = 1 $$

The second operation (·) satisfies all the conditions of a division ring.

Hence, the ring (R,+,·) is a division ring (skew field).

Note: In this specific case, since multiplication is commutative, it actually forms a field.

And so on.