Semigroups

What is a Semigroup?

A semigroup is an algebraic structure (S,*) that consists of a set S and a binary operation S×S→S, called the composition operation. This operation satisfies the associative property, meaning that $$ (a*b)*c = a*(b*c) \ \ \ \forall \ a, b, c \ \in S $$

It can also be referred to as a pseudogroup.

Semigroups do not require the presence of a neutral or inverse element.

If the semigroup includes a neutral element, it is known as a monoid.

Example

Take, for instance, the set of natural numbers N combined with the addition operation +.

$$ (N, +) $$

This set-up forms a groupoid because it involves an internal binary operation.

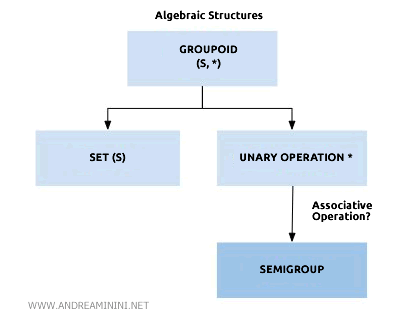
Moreover, it also constitutes a semigroup because the operation is associative.

For any three natural numbers a, b, and c, addition is associative:

$$ a + (b + c) = (a + b) + c $$

For example, if a=2, b=3, c=4:

$$ 2 + (3 + 4) = (2 + 3) + 4 = 9 $$

And so forth.