Groupoids

What is a groupoid?

A groupoid (or magma) is an algebraic structure defined by a non-empty set S and a closed binary operation S×S→S.

In abstract algebra, the groupoid serves as the foundational structure from which all other structures are derived.

Additional axioms are introduced to create various other algebraic structures from groupoids.

Note: If the operation in a groupoid involves addition, it is known as an additive groupoid (S,+). If it involves multiplication, we refer to it as a multiplicative groupoid (S,*).

When the operation of a groupoid also meets the associative property, it qualifies as a pseudogroup or semigroup.

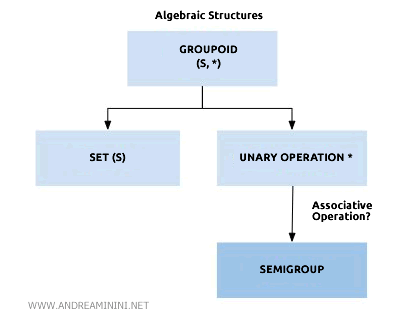
Should there be an inverse element, we then speak of a quasigroup.

A Practical Example

Example 1

The structure (N,+) exemplifies a groupoid.

It comprises the set of natural numbers N and the operation of addition (+).

Given any two elements from the set of natural numbers, their sum remains a natural number:

$$ a+b \ \in N \ \ \ \ \ \ \forall \ a,b \in N $$

The addition operation (+) is a closed operation within the set of natural numbers N.

Note: Another groupoid example is the structure (N,*), where multiplication also constitutes a closed operation in the natural numbers.

Example 2

The structure (N,-) does not qualify as a groupoid because subtraction does not operate internally within the set of natural numbers.

For example:

$$ 4 - 5 = -1 \notin N $$

Note: However, subtraction does form a groupoid with the set of integers (Z,-) since subtraction operates internally within the integers.

And so on.