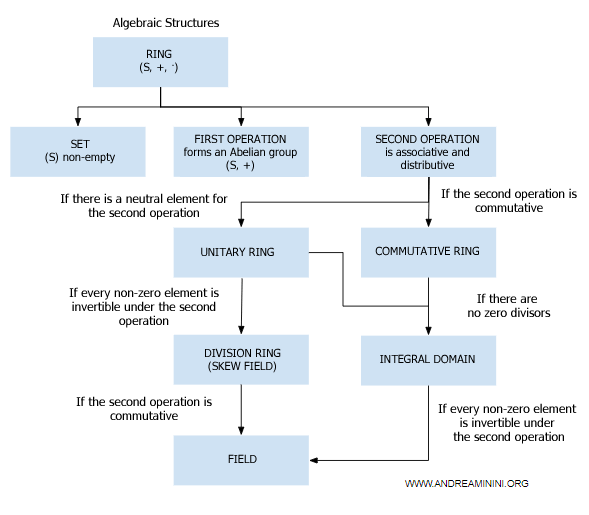
Field mathematics

A field is a non-empty set K, equipped with two internal binary operations (addition and multiplication), represented by + and · $$ (\ K \ , \ + \ , \ \cdot \ ) $$, which satisfy the following properties:

1. Commutative property $$ x+y=y+x $$ $$ x·y=y·x $$
2. Associative property $$ (x+y)+z = x+(y+z) $$ $$ (x·y)·z = x·(y·z) $$
3. Distributive property of multiplication over addition $$ (x+y)·z = (x·z)+(y·z) $$ $$ x·(y+z) = (x·y)+(x·z) $$
4. Additive identity
   There is at least one additive identity element such that for every element x in the set K, $$ 0+x = x+0 = x \ \ \ \ \forall x \in K $$
5. Multiplicative identity
   There is at least one multiplicative identity element such that for every element x in the set K, $$ 1·x = x·1 = x \ \ \ \ \forall x \in K $$
6. Additive inverse (opposite element)
   For every element x in the set K, there exists an opposite element -x such that their sum is the additive identity $$ x+(-x) = 0 \ \ \ \ \forall x \in K $$
7. Multiplicative inverse
   For every non-zero element \(x \neq 0\) in the set K, there exists a multiplicative inverse \(x^{-1}\) such that their product is the multiplicative identity $$ x \cdot x^{-1} = x^{-1} \cdot x = 1 \ \ \ \ \forall x \in K $$

Note. Simply put, a field is a ring (S,+,*) where the second operation, * (multiplication), is also commutative, there is a multiplicative identity, and every non-zero element of S has a multiplicative inverse.

A field where the elements are numbers is called a numeric field (or field of numbers).

The numeric field is a special case of a general field, which can be defined over any type of elements (e.g., numbers, polynomials, functions, or other algebraic entities).

A practical example

Consider the set of rational numbers Q with addition (+) and multiplication (·).

$$ (Q, + , \cdot ) $$

To determine whether this algebraic structure is a field, we need to verify if both operations meet the required properties.

The first operation (+)

Let's check whether the first operation forms an Abelian group (Q,+).

• Addition is an internal operation on Q $$ \forall \ a,b \in Q \ \ \ \ a+b \in Q $$
• Addition satisfies the associative property $$ \forall \ a,b,c \in Q \ \ \ (a+b)+c = a+(b+c) $$
• There is an additive identity $$ \forall \ a \in Q \ \ \ a + 0 = 0+a = a $$
• Every element in Q has an additive inverse $$ \forall \ a \in Q \ \ \ a + (-a) = (-a)+a = 0 $$

Therefore, addition forms a group (Q,+) with the set of rational numbers.

Moreover, since addition is commutative in the set of rational numbers, the group (Q,+) is an Abelian group.

$$ \forall \ a,b \in Q \ \ \ a+b = b+a $$

The first operation (+) meets all the conditions for a field.

The second operation (·)

Next, we check if the second operation · on Q satisfies the properties of a field.

• Multiplication is an internal operation on Q $$ \forall \ a,b \in Q\ \ \ \ a \cdot b \in Q $$
• Multiplication satisfies the distributive property with respect to addition, from both the left and the right $$ \forall \ a,b,c \in Q \ \ \ \ a \cdot (b+c) = ab+ac $$ $$ \forall \ a,b,c \in Q \ \ \ \ (a+b) \cdot c = ac+bc $$
• Multiplication satisfies the associative property $$ \forall \ a,b,c \in Q \ \ \ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$
• There is a multiplicative identity $$ \forall \ a \in Q \ \ \ a \cdot 1 = 1 \cdot a = a $$
• For every non-zero element in Q, there is a multiplicative inverse $$ \forall \ a \in Q \ , \ a \ne 0 \ \ \ a \cdot a^{-1} = a^{-1} \cdot a = 1 $$

Multiplication also satisfies the commutative property.

$$ \forall \ a,b \in Q\ \ \ \ a+b = b+a $$

The second operation (·) meets all the conditions for a field as well.

Thus, the ring (Q,+,·) is a field.

Commutative fields

A field is called commutative if the order of addition or multiplication does not affect the outcome.

Generally, most fields are commutative.

Example

The field of real numbers is commutative because the order in which you perform addition or multiplication does not change the result.

For instance:

$$ (3 + 4) = (4 + 3) = 7 $$

$$ (2 \cdot 5) = (5 \cdot 2) = 10 $$

Further notes

Some additional points about fields:

• A field is also known as a commutative division ring
  A field is also called a "commutative division ring" because it's a division ring where multiplication is commutative. In other words, every non-zero element has a multiplicative inverse, and the multiplication between any two elements satisfies the commutative property: \(a \cdot b = b \cdot a\). This distinguishes a field from a general division ring, which may not have commutative multiplication. Therefore, a field is a specific type of division ring.
• Difference between a general field and a numeric field
  The distinction between a "general field" and a "numeric field" is subtle, yet significant in mathematical contexts. A numeric field is a special case of a general field, where all elements are numbers. Therefore, while a numeric field is always a field, not every field is a numeric field.

And so on.