Integral Domains

An integral domain is a commutative and unital ring (S, +, ·) that has no zero divisors. $$ \forall \ a, b \in S \ , \ ab=0\ \Rightarrow\ (a=0\ \lor\ b=0) $$

In simpler terms, an integral domain is a commutative ring in which the product of two elements is zero only if at least one of them is zero.

To verify whether a commutative ring (S, +, ·) is an integral domain, we must demonstrate that there are no zero divisors in the set S.

What is a zero divisor? In a commutative ring (S, +, ·), a non-zero element a ≠ 0 in set S is called a zero divisor if there exists another non-zero element b ≠ 0 in set S such that ab = 0.

A Practical Example

The set of integers Z forms a ring (Z, +, ·) with respect to addition and multiplication.

$$ (Z,+,\cdot) $$

This is a commutative ring because multiplication also satisfies the commutative property.

The product of two non-zero integers a ≠ 0 and b ≠ 0 is always non-zero.

$$ \forall \ a,b \in Z \ , \ a \ne 0 \ , \ b \ne 0 \ \ \Longrightarrow \ \ ab \ne 0 $$

Note. If two integers have the same sign (positive or negative), their product is always positive. If they have different signs, their product is negative. Therefore, if the product of two integers is zero $$ ab = 0 $$ at least one of the factors must be zero. $$ a \cdot 0 = 0 \cdot a = 0 $$

As a result, there are no zero divisors in the set Z.

This means that the commutative ring (Z, +, ·) is an integral domain.

Example 2

Now, let's consider the set of residue classes modulo 6.

$$ Z_6 = \{ 0,1,2,3,4,5 \} $$

The set Z₆ forms a commutative ring (Z₆, +, ·) with respect to addition (+) and multiplication (·).

$$ (Z_6,+, \cdot) $$

To check for zero divisors, we can construct the multiplication table for the ring.

a ·6 b	0	1	2	3	4	5
0	0	0	0	0	0	0
1	0	1	2	3	4	5
2	0	2	4	0	2	4
3	0	3	0	3	0	3
4	0	4	2	0	4	2
5	0	5	4	3	2	1

In this case, there are three zero divisors: the numbers 2, 3, and 4.

For instance, the product 2·3 equals zero because the remainder is zero.

$$ 2 \cdot 3 \equiv 0 \ \text{mod} \ 6 $$

Explanation. To calculate the product of 2 and 3: $$ 2 \cdot 3 = 6 $$ Now, I find the remainder of dividing the result (2·3=6) by 6: $$ 6 \div 6 = 1 \ \text{remainder} = 0 $$ The remainder is zero, so in the modulo 6 system, 2·3=0. The same applies to the product 3·2=0.

Thus, because zero divisors exist, the commutative ring (Z₆, +, ·) is not an integral domain.

In general, a commutative group Z_n is an integral domain only if the number of elements (n) is a prime number.

Example 3

Now, consider the set of residue classes modulo 7.

$$ Z_7 = \{ 0,1,2,3,4,5,6 \} $$

In this case, the number of elements is prime (n=7).

The set Z₇ forms a commutative ring (Z₇, +, ·) with respect to addition (+) and multiplication (·).

$$ (Z_7,+, \cdot) $$

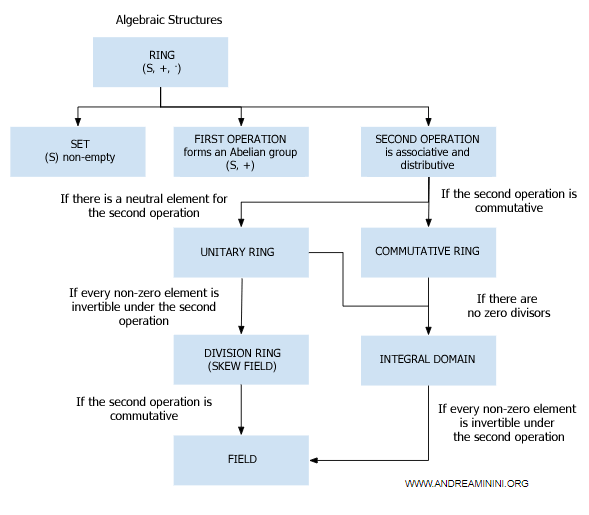
Let's create the multiplication table to check for zero divisors.

a ·7 b	0	1	2	3	4	5	6
0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6
2	0	2	4	6	1	3	5
3	0	3	6	2	5	1	4
4	0	4	1	5	2	6	3
5	0	5	3	1	6	4	2
6	0	6	5	4	3	2	1

In this case, there are no zero divisors.

Therefore, the commutative ring (Z₇, +, ·) is an integral domain.

Remarks

Here are some key points about integral domains:

• If the multiplicative inverse (second operation) exists for every non-zero element, the integral domain is a field.

  

• A finite integral domain is also a field

  An integral domain becomes a field if all elements are invertible under multiplication (the second operation).

  Proof. Consider an integral domain (D, +, ·) with a finite number of n distinct elements: $$ D=\{ a_1,a_2, ..., a_n \} $$ It's important to note that all elements are distinct.

  Example. To see how this works with numbers, let’s use the finite set Z₇ $$ D=\{0,1,2,3,4,5,6 \} $$ and the integral domain (Z₇, +, ·).
  

  Let’s take any non-zero element a_k in D (a_k ≠ 0). $$ a_k \ne 0 $$ Now, construct a function that multiplies a_k by every other element: $$ f: a_k \cdot a_i $$ Since we get distinct products, the function f is injective. Because D is finite, f is also surjective.

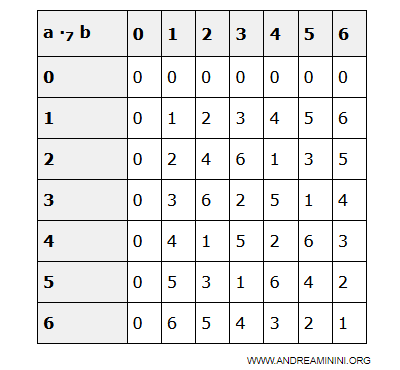
  Example. If we choose a_k = 5 in Z₇, the products with the other elements of Z₇ are all distinct.
  

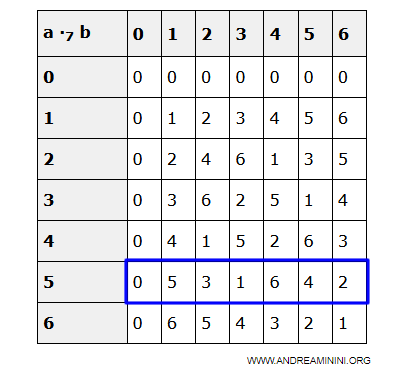
  This means that a_k must be equal to the product of a_k with some element a₀ in D $$ a_k = a_k \cdot a_0 = a_0 \cdot a_k $$

  Example. In this numerical example, if a_k = 5, then a₀ = 1 because $$ 5 = 5 \cdot 1 = 1 \cdot 5 $$
  

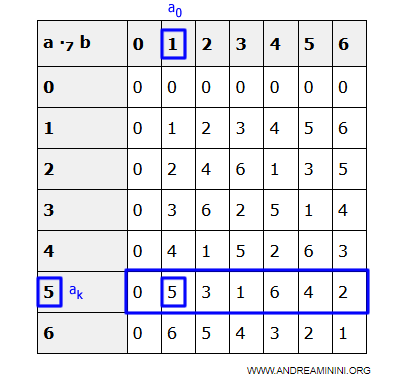
  Thus, any element x in D is equal to the product of a_k and some a_i $$ x = a_k \cdot a_i $$

  Example. Look at the multiplication table for Z₇. The product of a_k = 5 with elements of Z₇ generates all elements of Z₇. $$ 5 \cdot 0 = 0 \\ 5 \cdot 1 = 5 \\ 5 \cdot 2 = 3 \\ 5 \cdot 3 = 1 \\ 5 \cdot 4 = 6 \\ 5 \cdot 5 = 4 \\ 5 \cdot 6 = 2 $$

  Since a_k = a_k · a₀, $$ x = ( a_k \cdot a_0 ) \cdot a_i $$ Using the commutative property: $$ x = ( a_0 \cdot a_k ) \cdot a_i $$ And by the associative property: $$ x = a_0 \cdot (a_k \cdot a_i) $$ Knowing that x = a_k · a_i: $$ x = a_0 \cdot x $$ Because multiplication is commutative in an integral domain, $$ x = a_0 \cdot x = x \cdot a_0 $$ Therefore, a₀ = 1 is the multiplicative identity in D $$ a_0 = 1 $$ This proves the existence of a multiplicative identity in D. Consequently, the identity element 1 exists in D and is equal to the product of a_k and some a_j: $$ 1 = a_k \cdot a_j $$

  Example. In the numerical example of Z₇, with a_k = 5 and a_j = 3, $$ 1 = 5 \cdot 3 $$ So, the inverse of a_k = 5 is a_k^-1 = 3.

  In conclusion, all non-zero elements in D are invertible.

  Example. In the numerical example of Z₇, all non-zero elements in Z₇ have inverses. For instance, the inverse of 1 is 1, the inverse of 2 is 4, the inverse of 3 is 5, the inverse of 4 is 2, the inverse of 5 is 3, and the inverse of 6 is 6.
  

  As a result, the integral domain (D, +, ·) is a field.

And so on.