Rings in abstract algebra

In this definition, I’ve used the set of real numbers R for simplicity. However, the set can be anything.

The first operation (+) and the second operation (·) must meet different conditions.

Specifically, the first operation of a ring must form an abelian group (R,+)

Note: In a ring, addition must be commutative, while multiplication doesn’t have to be. Moreover, a ring must have an identity element and an additive inverse for addition, but there’s no requirement for multiplication to have an identity or an inverse. The order of operations is also crucial when defining a ring. For example, the structure (R,+,·) is a ring, but (R,·,+) is not, because zero doesn’t have an inverse. In other words, (R,+) forms an abelian group, while (R,·) doesn’t even form a group, let alone an abelian one.

It’s also conventional to refer to the first operation as "addition" and the second as "multiplication."

However, these operations don’t necessarily have to be literal addition and multiplication - they could represent other operations.

A practical example

The set of square matrices M_n(Z) of order n (i.e., n rows and n columns) forms a ring over the set of integers Z, with element-wise addition and row-by-column multiplication:

$$ (M_n(Z),+, \cdot) $$

Both operations are closed, meaning the result is always a square matrix.

$$ M_n(Z) \ × \ M_n(Z) \rightarrow M_n(Z) $$

Let’s check if the other properties are also satisfied.

The first operation

Element-wise addition of two square matrices satisfies the commutative property:

$$ A + B = B + A \ \ \ \forall \ A, B \in M_n(Z) $$

It also satisfies the associative property:

$$ (A + B) + C = A + (B + C) \ \ \ \forall \ A, B, C \in M_n(Z) $$

The additive identity exists: it’s the zero matrix.

And for every square matrix, an additive inverse exists:

$$ A + (-A) = 0 \ \ \ \forall \ A \in M_n(Z) $$

So, all the properties for the first operation of a ring are satisfied.

Note: The structure (M_n(Z),+) forms a group because the set is non-empty, the operation is closed, it satisfies associativity, and there exists both an identity and an inverse element for every element. Additionally, since it satisfies commutativity, (M_n(Z),+) forms an abelian group.

The second operation

The second operation is row-by-column matrix multiplication.

It satisfies the associative property:

$$ (A \cdot B) \cdot C = A \cdot (B \cdot C) \ \ \ \forall \ A, B, C \in M_n(Z) $$

It also satisfies the distributive property:

$$ (A + B) \cdot C = A \cdot C + B \cdot C \ \ \ \forall \ A, B, C \in M_n(Z) $$

$$ A \cdot ( B + C ) = A \cdot B + A \cdot C \ \ \ \forall \ A, B, C \in M_n(Z) $$

Thus, the second operation satisfies all the properties of a ring.

Conclusion

In conclusion, both operations meet all the requirements of a ring.

Therefore, the algebraic structure (M_n(Z),+,*) is a ring.

Types of rings

Rings may also satisfy additional, non-mandatory properties:

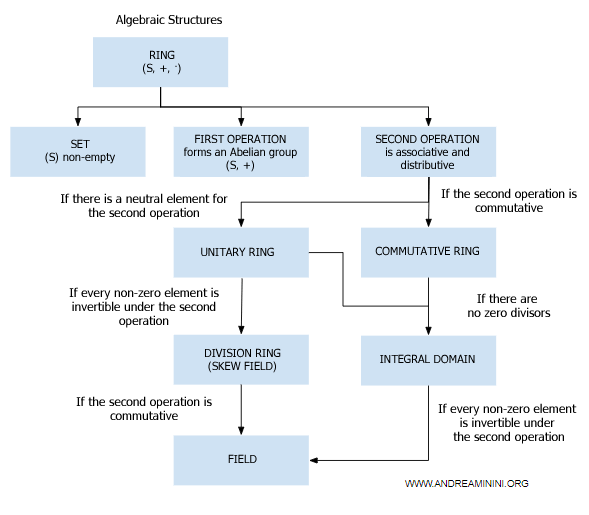
These include:

• Commutative ring
  A ring (R,+,·) is commutative if multiplication is also commutative: $$ a \cdot b = b \cdot a \ \ \forall \ a,b \in R $$
• Unital ring
  A ring (R,+,·) is unital if there exists a multiplicative identity element: $$ a \cdot 1 = 1 \cdot a = a \ \ \forall \ a \in R $$
• Integral domain
  A ring is an integral domain if it is commutative, unital, and contains no zero divisors: $$ \forall \ a,b \in R \ \ ab = 0 \ \Rightarrow \ a = 0 \ \text{or} \ b = 0 $$
• Division ring
  A division ring (R,+,·) is unital and has a multiplicative inverse for every non-zero element in R: $$ a \cdot a^{-1} = 1 \ \ \forall \ a \neq 0 \in R $$
• Field
  A field (R,+,·) is a commutative, unital ring where every non-zero element has a multiplicative inverse: $$ a \cdot a^{-1} = 1 \ \ \forall \ a \neq 0 \in R $$