Isomorphism Between Rings
An isomorphism between two rings A and A' is a bijective map φ such that: $$ \phi(a + b) = \phi(a) + \phi(b) \quad \forall \ a, b \in A $$ $$ \phi(a \cdot b) = \phi(a) \cdot \phi(b) \quad \forall \ a, b \in A $$ Here, a and b are elements of the ring A, while φ(a + b) and φ(ab) are elements of the ring A'.
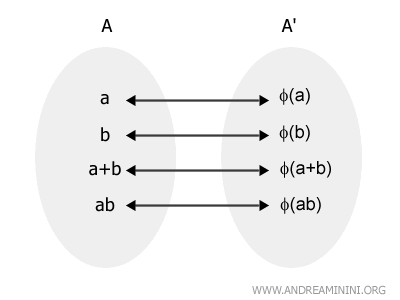
When such a map exists, the two rings are said to be isomorphic.
$$ A \simeq A' $$
This defines an equivalence relation: the two algebraic structures share the same algebraic properties.
In such cases, we say the two algebraic structures belong to the same isomorphism class.
A Concrete Example
Consider the set of complex numbers ℂ and the function that maps a complex number z = a + bi to its complex conjugate z'
$$ z' = \operatorname{Re}(z) - \operatorname{Im}(z) \cdot i $$
This function pairs each complex number z ∈ ℂ with another element of ℂ, and the correspondence is bijective.
Therefore, this map defines an isomorphism from ℂ onto itself.
For instance, take the two complex numbers:
$$ z_1 = 3 + 4i $$
$$ z_2 = 5 - 2i $$
Their conjugates under the mapping are:
$$ z'_1 = \operatorname{Re}(z_1) - \operatorname{Im}(z_1) \cdot i = 3 - 4i $$
$$ z'_2 = \operatorname{Re}(z_2) - \operatorname{Im}(z_2) \cdot i = 5 + 2i $$
Conversely, starting from the conjugates z′1 = 3 - 4i and z′2 = 5 + 2i, we can recover the original numbers:
$$ z_1 = \operatorname{Re}(z'_1) - \operatorname{Im}(z'_1) \cdot i = 3 + 4i $$
$$ z_2 = \operatorname{Re}(z'_2) - \operatorname{Im}(z'_2) \cdot i = 5 - 2i $$
This one-to-one correspondence also preserves addition. For example:
$$ z_1 + z_2 = (3 + 4i) + (5 - 2i) = 8 + 2i $$
$$ (z_1 + z_2)' = \operatorname{Re}(z_1 + z_2) - \operatorname{Im}(z_1 + z_2) \cdot i = 8 - 2i $$
$$ z_1 + z_2 = \operatorname{Re}[(z_1 + z_2)'] - \operatorname{Im}[(z_1 + z_2)'] \cdot i = 8 + 2i $$
The correspondence also respects multiplication:
$$ z_1 \cdot z_2 = (3 + 4i)(5 - 2i) = 15 - 6i + 20i - 8i^2 = 23 + 14i $$
$$ (z_1 \cdot z_2)' = \operatorname{Re}(z_1 \cdot z_2) - \operatorname{Im}(z_1 \cdot z_2) \cdot i = 23 - 14i $$
$$ z_1 \cdot z_2 = \operatorname{Re}[(z_1 \cdot z_2)'] - \operatorname{Im}[(z_1 \cdot z_2)'] \cdot i = 23 + 14i $$
And so on.
