Complex Numbers

What Are Complex Numbers?

A complex number \( z \) is an ordered pair of real numbers \( (a, b) \), defined with the following properties: $$ z = (a, b) $$ $$ (a, b) = (c, d) \: \text{if and only if} \: a = c \: \text{and} \: b = d $$ $$ (a, b) + (c, d) = (a + c, b + d) $$ $$ (a, b) \cdot (c, d) = (ac - bd, ad + bc) $$

Here, \( a \) and \( b \) are real numbers.

• The number \( a \) is called the real part of the complex number: $$ Re(z) = a $$
• The number \( b \) is called the imaginary part of the complex number: $$ Im(z) = b $$

Why Study Complex Numbers? Certain problems cannot be solved within the set of real numbers \( \mathbb{R} \). For instance, the square root of \(-4\) is undefined in \( \mathbb{R} \), as no real number squared equals a negative value.

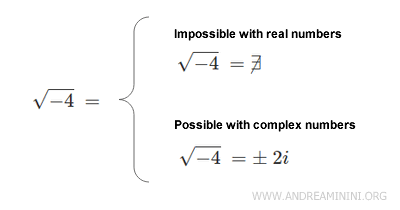
However, the square root of a negative number can be solved using the set of complex numbers \( \mathbb{C} \). More broadly, the set of complex numbers extends beyond the real numbers, enabling calculations that are otherwise impossible with \( \mathbb{R} \).

Each complex number belongs to the set \( \mathbb{R} \times \mathbb{R} \) because it consists of an ordered pair \( (a, b) \) of real numbers.

In fact, every complex number can be represented as a point on the Cartesian plane.

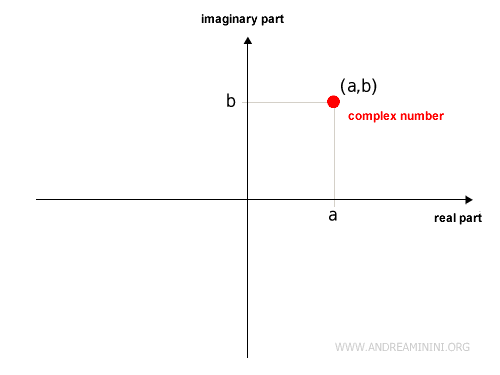
For every point on the plane, there is a corresponding complex number, and vice versa.

Note: There is no universal rule to determine whether one point on the plane is greater or less than another. We can only establish whether two points are equal or different. Therefore, it is not possible to compare complex numbers in terms of greater or lesser. A complex number is equal to another only if their real and imaginary parts are identical.

Algebraic Form of Complex Numbers

A complex number can also be expressed in algebraic (or compact) form as the sum of a real number \( a \) and an imaginary number \( i \cdot b \): $$ z = a + i \cdot b $$

Let’s begin with the algebraic form:

$$ z = a + i \cdot b $$

Here, \( a \) and \( b \) are real numbers.

Since they are real, they can be rewritten as \( (a, 0) \) and \( (b, 0) \):

$$ z = (a, 0) + i \cdot (b, 0) $$

The term \( i \), known as the imaginary unit, is defined as \( i = (0, 1) \), while \( b \) serves as the real coefficient of the imaginary part.

Substituting \( i = (0, 1) \):

$$ z = (a, 0) + (0, 1) \cdot (b, 0) $$

Using the formula for multiplying complex numbers, \( (x_1, y_1)(x_2, y_2) = (x_1x_2 - y_1y_2, x_1y_2 + x_2y_1) \):

$$ z = (a, 0) + (0 \cdot b - 1 \cdot 0, 0 \cdot 0 + 1 \cdot b) $$

$$ z = (a, 0) + (0 - 0, 0 + b) $$

$$ z = (a, 0) + (0, b) $$

$$ z = (a + 0, 0 + b) $$

$$ z = (a, b) $$

The final result is the complex number \( (a, b) \).

What Is an Imaginary Number? An imaginary number is a multiple of the imaginary unit \( i = (0, 1) \). It is a complex number of the form \( (0, a) \), where the real part is zero. For example, \( i \cdot 3 \) corresponds to the imaginary number \( (0, 3) \). More generally, \( i \cdot k \) represents an imaginary number of the form \( (0, k) \), where \( k \) is the coefficient of the imaginary part and \( i \) is the imaginary unit. This process also works in reverse: starting with a complex number \( (a, b) \), we can convert it into the algebraic form \( a + b \cdot i \): $$ (a, b) = (a, 0) + (0, b) = (a, 0) + (b, 0) \cdot i = a + b \cdot i $$

The set of complex numbers, denoted by \( \mathbb{C} \), is an extension of the set of real numbers.

Complex numbers are particularly useful in physics for analyzing periodic and sinusoidal phenomena.

A Practical Example

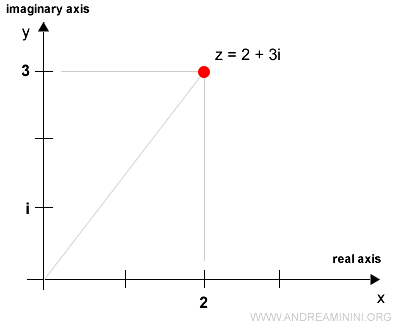
Consider the complex number \( z \):

$$ z = 2 + 3i $$

This number can be represented as Cartesian coordinates, where \( x = 2 \) and \( y = 3 \):

$$ (x, y) = (2, 3) $$

$$ (x, y) = (2, 0) + (0, 3) $$

In the context of complex numbers, \( (0, 3) \) can be expressed as:

$$ (0, 3) = (0, 1) \cdot (3, 0) $$

Substituting \( (0, 3) \) with \( (0, 1) \cdot (3, 0) \), we have:

$$ (x, y) = (2, 0) + (0, 3) $$

$$ (x, y) = (2, 0) + (0, 1) \cdot (3, 0) $$

Since the imaginary unit \( i \) is defined as \( (0, 1) \), this becomes:

$$ (x, y) = (2, 0) + i \cdot (3, 0) $$

Pairs where one element is zero correspond to real numbers.

By substituting \( (2, 0) = 2 \) and \( (3, 0) = 3 \), we recover the algebraic form of the complex number:

$$ (x, y) = 2 + i \cdot 3 $$

The graphical representation of this complex number on the Cartesian plane (commonly referred to as the complex plane or Gauss plane) is shown below:

Imaginary Unit, Real Part, and Imaginary Part

The imaginary unit of complex numbers is the pair \( (0, 1) \). In compact or algebraic form, it is denoted by the symbol \( i \) (or sometimes \( j \)): $$ i = (0, 1) $$

Pairs of numbers where one coordinate is zero correspond to real numbers:

$$ (a, 0) = a $$

$$ (0, b) = b $$

The pair \( (0, 1) \) is particularly significant because squaring it yields \( -1 \):

$$ (0, 1) \cdot (0, 1) = (0 \cdot 0 - 1 \cdot 1, 0 \cdot 1 + 1 \cdot 0) = (-1, 0) = -1 $$

This property enables us to solve equations like \( x^2 = -1 \).

Note: The imaginary unit satisfies \( i^2 = (0, 1) \cdot (0, 1) = -1 \). As a result, the product of two complex numbers can be expressed as: $$ z_1 \cdot z_2 = (a + bi)(c + di) = ac + adi + bic + bd^2 = ac + adi + bic - bd = (ac - bd) + (ad + bc)i $$

This pair is referred to as the imaginary unit \( i \) in complex numbers.

$$ (a, b) = (a, 0) + (0, b) $$

Here, \( (0, b) \) can be derived as the product \( (0, 1) \cdot (b, 0) \):

$$ (a, b) = (a, 0) + (0, 1) \cdot (b, 0) $$

Since \( (a, 0) \) and \( (b, 0) \) are real numbers, the compact form of the complex number becomes:

$$ z = a + i \cdot b $$

In this expression, \( a \) represents the real part of the complex number, \( b \) is the imaginary part, and \( i \) is the imaginary unit.

Purpose of Complex Numbers

Complex numbers were introduced to solve problems that are impossible to resolve within the realm of rational numbers.

Example 1

Consider the following equation, which has no real solutions because the square root of a negative number is undefined in the real number system:

$$ x^2 = -1 $$

With complex numbers, however, it becomes solvable:

$$ x^2 = (-1, 0) $$

In the complex number system, \( (-1, 0) \) is obtained as the product \( (0, 1) \cdot (0, 1) \):

$$ (-1, 0) = (0, 1) \cdot (0, 1) $$

Substituting \( (-1, 0) \) with \( (0, 1) \cdot (0, 1) \):

$$ x^2 = (0, 1) \cdot (0, 1) $$

Since \( (0, 1) \) is the imaginary unit \( i \):

$$ x^2 = i \cdot i $$

$$ x^2 = i^2 $$

Taking the square root of both sides gives:

$$ \sqrt{x^2} = \sqrt{i^2} $$

$$ x = i $$

We can rewrite the solution \( i \) in its algebraic form:

$$ x = 0 + i $$

Thus, the problem is solved.

Example 2

Consider a quadratic equation in \( z \):

$$ az^2 + bz + c = 0 $$

This equation has two real solutions if \( b^2 - 4ac \geq 0 \):

$$ \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \begin{cases} z_1 \\ z_2 \end{cases} $$

The coefficients \( a, b, c \) relate to the solutions \( z_1 \) and \( z_2 \) as follows:

$$ z_1 + z_2 = -\frac{b}{a} $$

$$ z_1 \cdot z_2 = \frac{c}{a} $$

However, not all quadratic equations have real solutions. For instance, the following equation:

$$ z^2 + 1 = 0 $$

has no solutions in the real number system, and the relationships between the coefficients cannot be satisfied:

$$ z_1 + z_2 = 0 $$

$$ z_1 \cdot z_2 = 1 $$

To ensure that every quadratic equation has a solution, we extend the real numbers \( \mathbb{R} \) to the complex numbers \( \mathbb{C} \) by introducing the imaginary unit \( z \):

$$ z = \pm \sqrt{-1} $$

Algebraically, this gives:

$$ z^2 = -1 $$

which satisfies both the equation \( z^2 + 1 = 0 \) and the relationships between the coefficients.

Addition and Multiplication of Complex Numbers

In the set of complex numbers, two operations are defined:

• Addition
  Addition is performed by summing the corresponding components of the pairs: $$ (a, b) + (c, d) = (a + c, b + d) $$

  Example: $$ (1, 2) + (2, 4) = (1 + 2, 2 + 4) = (3, 6) $$

• Multiplication
  The formula for multiplication is less intuitive but becomes clear when you understand the role of the imaginary unit: $$ (a, b) \cdot (c, d) = (ac - bd, ad + bc) $$

  Example: $$ (1, 2) \cdot (2, 4) = (1 \cdot 2 - 2 \cdot 4, 1 \cdot 4 + 2 \cdot 2) = (-6, 8) $$

In both cases, the result is another complex number.

Note: Subtraction is performed similarly to addition: $$ (a, b) - (c, d) = (a - c, b - d) $$ Division, on the other hand, requires reducing the problem to multiplication: $$ \frac{a + bi}{c + di} = \frac{a + bi}{c + di} \cdot \frac{c - di}{c - di} = \frac{ac - adi + bic - bdi^2}{c^2 - cdi + cdi - d^2i^2} = \frac{(ac + bd) + i(bc - ad)}{c^2 + d^2} $$ Simplifying, this becomes: $$ \frac{ac + bd}{c^2 + d^2} + i \cdot \frac{bc - ad}{c^2 + d^2} $$

Comparing Complex Numbers

Two complex numbers are equal if and only if their real parts and imaginary parts are identical.

However, it is not possible to establish an order relation to compare distinct complex numbers.

In other words, you cannot state that one complex number is greater or less than another, because each complex number is composed of a pair of real numbers.

Example

Consider the following three complex numbers:

$$ z_1 = 5 + 3i $$

$$ z_2 = 4 + 2i $$

$$ z_3 = 5 + 3i $$

We can say that \( z_1 \) and \( z_3 \) are equal because they share the same real part (5) and the same imaginary part (3i).

On the other hand, \( z_1 \) and \( z_2 \) are distinct, but it is not possible to determine whether one is greater or smaller than the other.

Note: The magnitude (or modulus) of complex numbers can be compared to evaluate their distance from the origin. However, this is not a comparison of the numbers themselves but rather their distances from the origin.

Cartesian and Polar Forms

Complex numbers can be represented in several forms:

• Cartesian form
  $$ s = \sigma + j\omega $$
• Trigonometric form
  $$ s = p (\cos \phi + j \sin \phi) $$
• Polar (or exponential) form
  $$ s = p e^{j\phi} $$

Here:

• \( \sigma \) is the real part
• \( \omega \) is the imaginary part
• \( p \) is the magnitude (or modulus)
• \( \phi \) is the argument of the complex number \( s \)

Note: The argument \( \phi \) must lie within the range \( -\pi \) to \( \pi \): $$ -\pi < \phi \leq \pi $$

Representation of Complex Numbers

Complex numbers can be represented on a Cartesian plane, known as the Gauss plane, with a real axis and an imaginary axis.

This is referred to as the algebraic form of complex numbers.

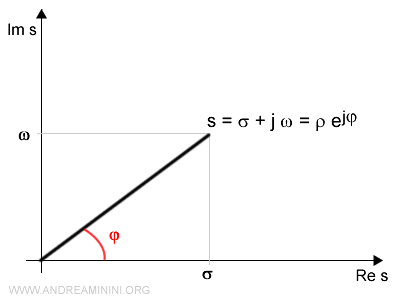
Complex numbers can also be expressed in trigonometric or polar form:

$$ z = p (\cos \phi + j \cdot \sin \phi) $$

To convert from polar to Cartesian form:

$$ \sigma = p \cdot \cos \phi $$

$$ \omega = p \cdot \sin \phi $$

The following relationships are valid: $$ p = \sqrt{\sigma^2 + \omega^2} $$ $$ \phi = \arctan \frac{\omega}{\sigma} = \arcsin \frac{\omega}{\sqrt{\sigma^2 + \omega^2}} $$

Complex numbers can also be represented in exponential form:

$$ z = p \cdot e^{j\phi} = p \cdot (\cos \phi + j \cdot \sin \phi) $$

This representation is derived from Euler's formula:

$$ e^{j\phi} = \cos \phi + j \cdot \sin \phi $$

Functions of a Complex Variable

A function of a complex variable is a function defined over the set of complex numbers: $$ f(z) $$ where $$ z = x + i \cdot y $$

Such a function can be expressed as:

$$ w = f(z) = u(\sigma, \omega) + i \cdot v(\sigma, \omega) $$

Here, \( u \) and \( v \) are real-valued functions representing the real and imaginary parts, respectively.

Example

The real function \( e^{iy} \) can be rewritten as a function of a complex variable, and vice versa:

$$ e^{iy} = \cos y + i \cdot \sin y $$

Here, \( i \) represents the imaginary unit.

This approach can also be applied to functions such as sine, cosine, square roots, and more.

Notes

Additional remarks about complex numbers:

• Real numbers are a subset of complex numbers
  A complex number with a zero imaginary part, such as \( (a, 0) \), is a real number and is called a "real complex number." Each such number corresponds uniquely to a point on the x-axis in the complex plane. For example, writing \( (2, 0) \) or simply \( 2 \) refers to the same point on the x-axis.
  
  Thus, every real number belongs to the set of complex numbers, meaning that the set of real numbers is a subset of the complex numbers: $$ \mathbb{R} \subseteq \mathbb{C} $$ Operations on real complex numbers yield results identical to operations on real numbers. This property highlights that the set of real numbers \( \mathbb{R} \) is isomorphic to the subset \( C' \subseteq \mathbb{C} \), consisting of pairs \( (a, 0) \), under addition and multiplication.

  Example: Adding two real complex numbers \( (2, 0) \) and \( (3, 0) \): $$ (2, 0) + (3, 0) = (5, 0) $$ This is the same result as adding their corresponding real numbers: $$ 2 + 3 = 5 $$ Similarly, multiplying these real complex numbers gives \( (6, 0) \): $$ (2, 0) \cdot (3, 0) = (2 \cdot 3 - 0 \cdot 0, 2 \cdot 0 + 0 \cdot 3) = (6, 0) $$ Again, this matches the product of their corresponding real numbers: $$ 2 \cdot 3 = 6 $$

• History of Complex Numbers
  In the 16th century, Rafael Bombelli was among the first to explicitly use imaginary numbers, referring to \( +i \) and \( -i \) as "plus of minus" (p.d.m.) and "minus of minus" (m.d.m.), respectively. He used them to calculate square roots of negative numbers. Initially, imaginary numbers were considered "wild quantities" or mathematical constructs—useful but not fully integrated into rigorous mathematics. Descartes coined the term "imaginary numbers" to emphasize their seemingly unreal nature. In the 18th century, Gauss introduced a geometric representation of complex numbers and proved the Fundamental Theorem of Algebra, establishing their significance in mathematics. Later, Hamilton (1833) formalized complex numbers as ordered pairs of real numbers \( (a, b) \), where \( a + bi \) represents any complex number. Over time, complex numbers found applications in numerous fields, such as electrical engineering, evolving from "imaginary tools" to a cornerstone of mathematics and technology.

And so on.