Dividing Two Complex Numbers in Exponential Form

Given two complex numbers in exponential form, \( z_1 = r_1 e^{i\alpha} \) and \( z_2 = r_2 e^{i\beta} \), their quotient, \( \frac{z_1}{z_2} \), is another complex number whose modulus is the ratio of the individual moduli, \( \frac{r_1}{r_2} \), and whose argument is the difference of the original arguments, \( \alpha - \beta \): $$ \frac{z_1}{z_2} = \frac{r_1 e^{i\alpha}}{r_2 e^{i\beta}} = \left( \frac{r_1}{r_2} \right) e^{i(\alpha - \beta)} $$

A Practical Example

Let's consider two complex numbers:

$$ z_1 = 1 + 3i $$

$$ z_2 = 4 + 2i $$

On the complex plane (Gauss plane), these numbers correspond to the points (1,3) and (4,2).

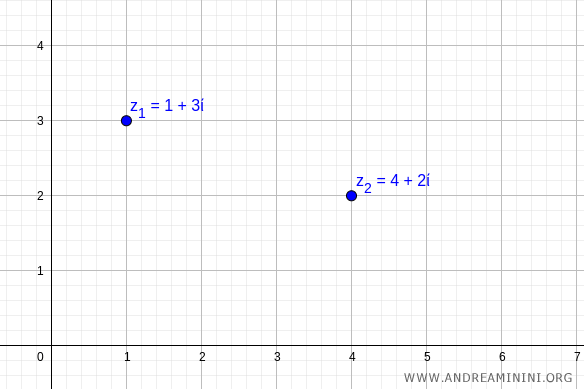
Next, we convert these numbers into their trigonometric form.

First, we compute their moduli:

$$ r_1 = \sqrt{1^2 + 3^2} = \sqrt{10} \approx 3.16 $$

$$ r_2 = \sqrt{4^2 + 2^2} = \sqrt{20} \approx 4.47 $$

Next, we determine their arguments:

$$ \alpha = \arctan \frac{3}{1} \approx 71.57^\circ $$

$$ \beta = \arctan \frac{2}{4} \approx 26.57^\circ $$

Thus, the trigonometric representations of \( z_1 \) and \( z_2 \) are:

$$ z_1 = 3.16 \left( \cos 71.57^\circ + i \sin 71.57^\circ \right) $$

$$ z_2 = 4.47 \left( \cos 26.57^\circ + i \sin 26.57^\circ \right) $$

The polar coordinates \([r, \alpha]\) of these complex numbers correspond to the same points on the Gauss plane.

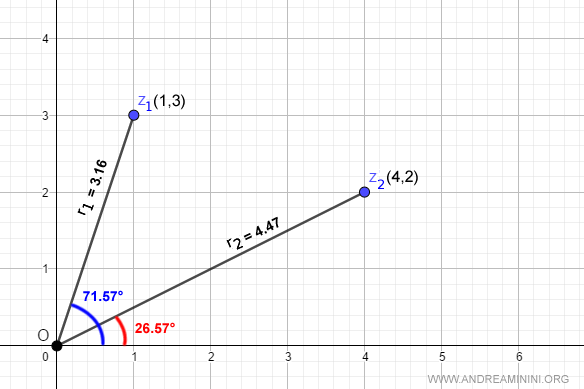
Now that we have their polar coordinates, we can express them in exponential form using Euler’s formula: \( z = r e^{i\alpha} \).

$$ z_1 = 3.16 e^{i 71.57^\circ} $$

$$ z_2 = 4.47 e^{i 26.57^\circ} $$

Now, we compute the division of these two complex numbers in exponential form:

$$ \frac{z_1}{z_2} = \frac{3.16}{4.47} e^{i (71.57^\circ - 26.57^\circ)} $$

$$ \frac{z_1}{z_2} = 0.71 e^{i 45^\circ} $$

We then rewrite the quotient in trigonometric form:

$$ \frac{z_1}{z_2} = 0.71 \left( \cos 45^\circ + i \sin 45^\circ \right) $$

Finally, we convert it into algebraic form by evaluating the sine and cosine:

$$ \frac{z_1}{z_2} = 0.71 \cos 45^\circ + 0.71 i \sin 45^\circ $$

$$ = 0.71 \times 0.71 + 0.71 i \times 0.71 $$

$$ = 0.5 + 0.5 i $$

The result is the quotient of the two complex numbers.

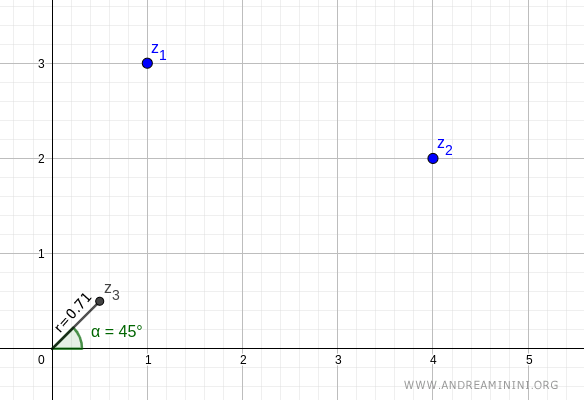
Verification. To verify the result, let's compute the division using the algebraic form:

$$ \frac{z_1}{z_2} = \frac{1+3i}{4+2i} $$

Multiply numerator and denominator by the conjugate of the denominator:

$$ \frac{z_1}{z_2} = \frac{(1+3i)(4-2i)}{(4+2i)(4-2i)} $$

Expanding both expressions:

$$ = \frac{4 - 2i + 12i - 6i^2}{16 - 8i + 8i - 4i^2} $$

Since \( i^2 = -1 \), we simplify:

$$ = \frac{4+10i - 6(-1)}{16 - 4(-1)} $$

$$ = \frac{4 + 10i + 6}{16 + 4} $$

$$ = \frac{10 + 10i}{20} $$

$$ = \frac{1 + i}{2} $$

$$ = 0.5 + 0.5i $$

Since we obtained the same result, our calculation is verified.

And so on.