n-th Root of a Complex Number

The n-th root $ \sqrt[n]{z} $ of a complex number $ z $ is any complex number $ w $ that satisfies the equation $ w^n = z $: $$ w = \sqrt[n]{z} \Longleftrightarrow w^n = z $$

To determine the n-th roots of a complex number \( z = a+bi \), it's best to express it in its trigonometric form:

$$ z = r \cdot \left( \cos \alpha + i \cdot \sin \alpha \right) $$

Using this representation, we can compute the n-th roots of the complex number as follows:

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot \left[ \cos \left(\frac{\alpha}{n} + \frac{2k\pi}{n} \right) + i \cdot \sin \left(\frac{\alpha}{n} + \frac{2k\pi}{n} \right) \right] $$

This formula yields all \( n \) distinct n-th roots of \( z \).

How Many n-th Roots Does a Complex Number Have?

Every complex number \( z \) has exactly \( n \) distinct n-th roots, which are evenly spaced around a circle of radius \( \sqrt[n]{r} \) in the complex plane.

Geometrically, these roots form the vertices of a regular n-sided polygon inscribed in the circle.

Among these, the principal root is the one corresponding to \( k = 0 \), meaning it has the smallest positive argument, given by dividing \( \alpha \) (the argument of \( z \)) by \( n \):

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot \left[ \cos \left(\frac{\alpha}{n} \right) + i \cdot \sin \left(\frac{\alpha}{n} \right) \right] $$

When referring to the "n-th root" in a strict sense, it usually means the principal root. The remaining \( n-1 \) roots can be obtained by adding multiples of \( \frac{2\pi}{n} \) to the argument:

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot \left[ \cos \left(\frac{\alpha}{n} + \frac{2k\pi}{n} \right) + i \cdot \sin \left(\frac{\alpha}{n} + \frac{2k\pi}{n} \right) \right], \quad k = 0, 1, \dots, n-1 $$

Note: Technically, the n-th roots of a complex number form an infinite sequence if we account for all possible rotations around the complex plane. Mathematically, these roots are given by: $$ \theta_k = \frac{\alpha}{n} + \frac{2k\pi}{n} + 2m\pi, \quad \text{where } k = 0, 1, \dots, n-1, \; m \in \mathbb{Z} $$ Since \( m \) can be any integer, this sequence extends indefinitely. In essence, each root reappears after every full \( 2\pi \) rotation. However, by convention, we usually focus only on the \( n \) distinct roots that lie within the first complete revolution (i.e., setting \( m = 0 \)).

A Practical Example

Let's consider the complex number:

$$ z = 16 \left(\cos \frac{3\pi}{4} + i \sin \frac{3\pi}{4}\right) $$

We need to compute the fourth roots (\( n = 4 \)) of \( z \).

Using the general formula for the n-th roots of a complex number:

$$ \sqrt[4]{z} = \sqrt[4]{r} \cdot \left[ \cos \left(\frac{\alpha}{4} + \frac{2k\pi}{4} \right) + i \sin \left(\frac{\alpha}{4} + \frac{2k\pi}{4} \right) \right] $$

Here, the modulus \( r \) of \( z \) is \( 16 \), and its argument \( \alpha \) is \( \frac{3\pi}{4} \).

Substituting these values:

$$ \sqrt[4]{z} = \sqrt[4]{16} \cdot \left[ \cos \left(\frac{\frac{3\pi}{4}}{4} + \frac{2k\pi}{4} \right) + i \sin \left(\frac{\frac{3\pi}{4}}{4} + \frac{2k\pi}{4} \right) \right] $$

Since \( \sqrt[4]{16} = 2 \), this simplifies to:

$$ \sqrt[4]{z} = 2 \cdot \left[ \cos \left(\frac{3\pi}{16} + \frac{2k\pi}{4} \right) + i \sin \left(\frac{3\pi}{16} + \frac{2k\pi}{4} \right) \right] $$

The Principal Root

The principal root, corresponding to \( k=0 \), is:

$$ w_0 = 2 \left[\cos\left(\frac{3\pi}{16}\right) + i \sin\left(\frac{3\pi}{16}\right)\right] $$

This is the primary fourth root of \( z \), and all other roots can be derived from it by adding successive multiples of \( \frac{\pi}{2} \) to the argument.

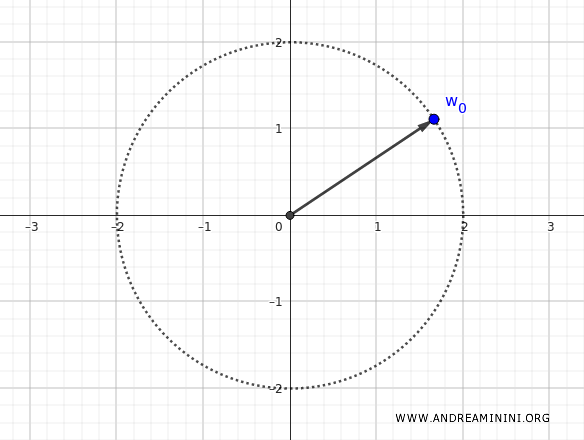
Computing the Remaining Roots

The remaining roots (\( k = 1, 2, 3 \)) are found by incrementing the argument in steps of \( \frac{\pi}{2} \).

Second Root (\( k = 1 \))

Adding \( \frac{\pi}{2} \) to the argument of \( w_0 \):

$$ w_1 = 2 \left[\cos\left(\frac{3\pi}{16} + \frac{\pi}{2}\right) + i \sin\left(\frac{3\pi}{16} + \frac{\pi}{2}\right)\right] $$

Computing the new angle:

$$ \frac{3\pi}{16} + \frac{\pi}{2} = \frac{3\pi}{16} + \frac{8\pi}{16} = \frac{11\pi}{16} $$

Thus,

$$ w_1 = 2 \left[\cos\left(\frac{11\pi}{16}\right) + i \sin\left(\frac{11\pi}{16}\right)\right] $$

Since the fourth roots are evenly spaced at 90° intervals, \( w_1 \) is located \( 90^\circ \) counterclockwise from \( w_0 \).

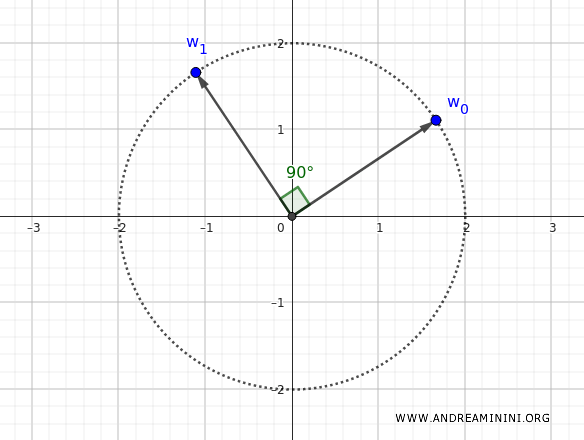
Third Root (\( k = 2 \))

Adding another \( \frac{\pi}{2} \) step:

$$ w_2 = 2 \left[\cos\left(\frac{3\pi}{16} + \pi\right) + i \sin\left(\frac{3\pi}{16} + \pi\right)\right] $$

Computing the angle:

$$ \frac{3\pi}{16} + \pi = \frac{3\pi}{16} + \frac{16\pi}{16} = \frac{19\pi}{16} $$

Thus,

$$ w_2 = 2 \left[\cos\left(\frac{19\pi}{16}\right) + i \sin\left(\frac{19\pi}{16}\right)\right] $$

Graphically, \( w_2 \) is positioned \( 180^\circ \) from \( w_0 \), directly opposite on the complex plane.

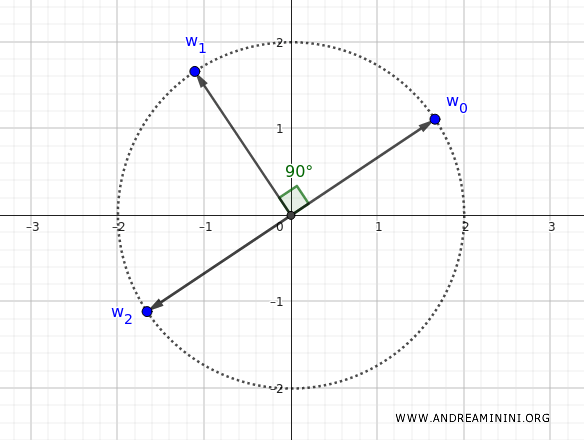
Fourth Root (\( k = 3 \))

Adding the final \( \frac{\pi}{2} \) step:

$$ w_3 = 2 \left[\cos\left(\frac{3\pi}{16} + \frac{3\pi}{2}\right) + i \sin\left(\frac{3\pi}{16} + \frac{3\pi}{2}\right)\right] $$

Computing the angle:

$$ \frac{3\pi}{16} + \frac{3\pi}{2} = \frac{3\pi}{16} + \frac{24\pi}{16} = \frac{27\pi}{16} $$

Thus,

$$ w_3 = 2 \left[\cos\left(\frac{27\pi}{16}\right) + i \sin\left(\frac{27\pi}{16}\right)\right] $$

This root completes the set, bringing us full circle.

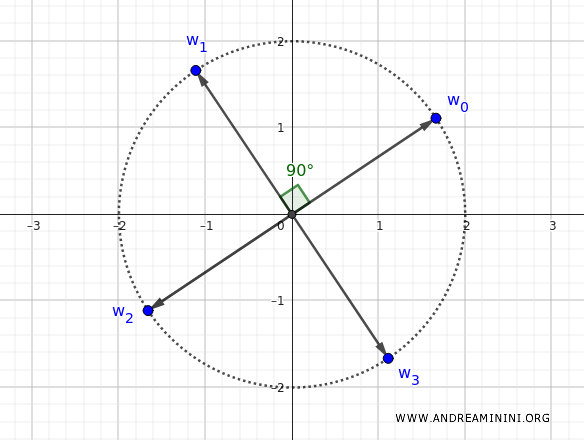
Final Recap

Note: The four roots are evenly spaced around the unit circle. While theoretically, additional rotations could be performed, they simply map back onto the same points. Thus, in practical applications, we typically focus on the first set of \( n = 4 \) distinct roots.

In summary, the four fourth roots of \( z \) are:

$$ w_0 = 2 \left[\cos\left(\frac{3\pi}{16}\right) + i \sin\left(\frac{3\pi}{16}\right)\right] $$

$$ w_1 = 2 \left[\cos\left(\frac{11\pi}{16}\right) + i \sin\left(\frac{11\pi}{16}\right)\right] $$

$$ w_2 = 2 \left[\cos\left(\frac{19\pi}{16}\right) + i \sin\left(\frac{19\pi}{16}\right)\right] $$

$$ w_3 = 2 \left[\cos\left(\frac{27\pi}{16}\right) + i \sin\left(\frac{27\pi}{16}\right)\right] $$

These represent the four solutions, symmetrically arranged in the complex plane.

Proof

Let’s consider a complex number \( z \):

$$ z = r ( \cos \alpha + i \sin \alpha ) $$

We assume that \( w \) is an n-th root of \( z \), meaning:

$$ w = s ( \cos \beta + i \sin \beta ) $$

Since \( w \) is an n-th root of \( z \), raising \( w \) to the power of \( n \) must yield \( z \):

$$ w^n = z $$

Expanding both sides:

$$ w^n = r ( \cos \alpha + i \sin \alpha ) $$

Applying De Moivre’s theorem to compute \( w^n \):

$$ [s ( \cos \beta + i \sin \beta )]^n = r ( \cos \alpha + i \sin \alpha ) $$

Using the exponentiation formula for complex numbers:

$$ s^n ( \cos n\beta + i \sin n\beta ) = r ( \cos \alpha + i \sin \alpha ) $$

By equating the moduli and arguments on both sides, we obtain:

$$ \begin{cases} s^n = r \\ \\ n \beta = \alpha \end{cases} $$

However, because angles in the complex plane are defined modulo \( 2\pi \), we must also consider the possibility of full rotations:

$$ \begin{cases} s^n = r \\ \\ n \beta = \alpha + 2\pi k, \quad k \in \mathbb{Z} \end{cases} $$

Solving for \( \beta \), we obtain:

$$ \beta = \frac{\alpha}{n} + \frac{2\pi k}{n} $$

Thus, we can rewrite our equations as:

$$ \begin{cases} s^n = r \\ \\ \beta = \frac{\alpha}{n} + \frac{2\pi k}{n} \end{cases} $$

Deriving the n-th Root Formula

From this, we conclude that the n-th roots of \( z \) are given by:

$$ \sqrt[n]{z} = \sqrt[n]{r ( \cos \alpha + i \sin \alpha)} $$

Using the property that the modulus and argument can be separated:

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot \sqrt[n]{\cos \alpha + i \sin \alpha} $$

Applying the formula for extracting n-th roots of a complex number:

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot \left( \cos \frac{\alpha}{n} + i \sin \frac{\alpha}{n} \right) $$

Since we must account for all possible rotations, the general solution becomes:

$$ \sqrt[n]{z} = \sqrt[n]{r} \cdot \left[ \cos \left( \frac{\alpha}{n} + \frac{2\pi k}{n} \right) + i \sin \left( \frac{\alpha}{n} + \frac{2\pi k}{n} \right) \right] $$

From our earlier derivation, we established that \( s^n = r \) and \( \beta = \frac{\alpha}{n} + \frac{2\pi k}{n} \), so we can write:

$$ \sqrt[n]{z} = \sqrt[n]{s^n} \cdot \left[ \cos ( \beta ) + i \sin ( \beta ) \right] $$

Taking the n-th root:

$$ \sqrt[n]{z} = s \cdot \left[ \cos ( \beta ) + i \sin ( \beta ) \right] $$

Since we initially defined \( w \) as:

$$ w = s \left[ \cos ( \beta ) + i \sin ( \beta ) \right] $$

we conclude that:

$$ \sqrt[n]{z} = w $$

Thus, we have rigorously shown that \( w \) is indeed an n-th root of \( z \).

Square Root of Negative Numbers

This approach also provides a natural way to define the square root of negative numbers using the trigonometric representation of complex numbers.

As an example, let’s compute the square roots of \(-4\) using this method.

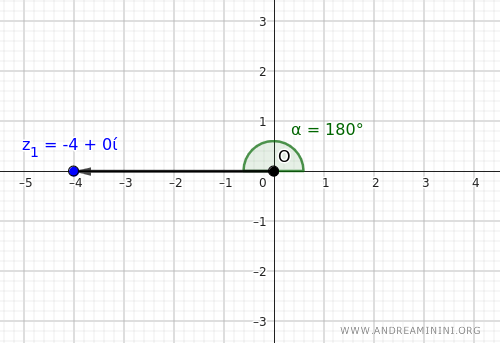
Expressing \(-4\) in Trigonometric Form

To apply this approach, we first express \( z = -4 \) in polar form:

• The modulus of \(-4\) is: $$ r = \lvert -4 \rvert = 4 $$
• The argument \( \alpha \), which is the angle between the number and the positive real axis, is: $$ \alpha = \pi \quad \text{(since \(-4\) lies on the negative real axis, corresponding to a 180° angle)} $$

Thus, we can write:

$$ -4 = 4 \cdot \left(\cos\pi + i\sin\pi\right) $$

Applying the Square Root Formula

Using the general formula for the n-th roots of a complex number, with \( n = 2 \):

$$ \sqrt[2]{z} = \sqrt[2]{r} \cdot \left[\cos\left(\frac{\alpha}{2} + k\frac{2\pi}{2}\right) + i\sin\left(\frac{\alpha}{2} + k\frac{2\pi}{2}\right)\right], \quad k = 0, 1 $$

Simplifying:

$$ \sqrt[2]{z} = \sqrt[2]{r} \cdot \left[\cos\left(\frac{\alpha}{2} + k \pi \right) + i\sin\left(\frac{\alpha}{2} + k \pi \right)\right], \quad k = 0, 1 $$

Substituting \( r = 4 \) and \( \alpha = \pi \):

$$ \sqrt[2]{-4} = \sqrt[2]{4} \cdot \left[\cos\left(\frac{\pi}{2} + k \pi \right) + i\sin\left(\frac{\pi}{2} + k \pi \right)\right], \quad k = 0, 1 $$

Since \( \sqrt[2]{4} = 2 \), this simplifies to:

$$ \sqrt[2]{-4} = 2 \cdot \left[\cos\left(\frac{\pi}{2} + k \pi \right) + i\sin\left(\frac{\pi}{2} + k \pi \right)\right], \quad k = 0, 1 $$

Computing the Two Square Roots

1. For \( k = 0 \): $$ w_0 = 2 \cdot \left[\cos\left(\frac{\pi}{2}\right) + i\sin\left(\frac{\pi}{2}\right)\right] $$ Evaluating: $$ w_0 = 2 \cdot \left[0 + i\cdot 1\right] $$ $$ w_0 = 2i $$
2. For \( k = 1 \): $$ w_1 = 2 \cdot \left[\cos\left(\frac{\pi}{2} + \pi\right) + i\sin\left(\frac{\pi}{2} + \pi\right)\right] $$ Expanding: $$ w_1 = 2 \cdot \left[\cos\left(\frac{3\pi}{2}\right) + i\sin\left(\frac{3\pi}{2}\right)\right] $$ Since \( \cos\left(\frac{3\pi}{2}\right) = 0 \) and \( \sin\left(\frac{3\pi}{2}\right) = -1 \), we obtain: $$ w_1 = 2 \cdot \left[0 - i\cdot 1\right] $$ $$ w_1 = -2i $$

Conclusion

Thus, the two square roots of \(-4\) are:

$$ w_0 = 2i \quad \text{and} \quad w_1 = -2i $$

By convention, the principal root is \( w_0 = 2i \), while the other root is \( w_1 = -2i \).

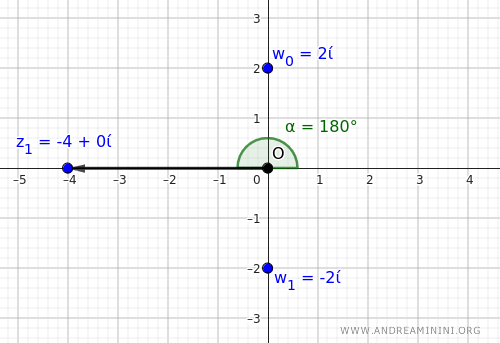
Both of these values satisfy the equation \( w^2 = -4 \), confirming our result.