Real Complex Numbers

A real complex number is a complex number in the form (a,0), where the imaginary part is zero.

The set of real complex numbers is equivalent to the set of real numbers.

Essentially, the set of real complex numbers corresponds to the x-axis (Re) on the Gaussian plane.

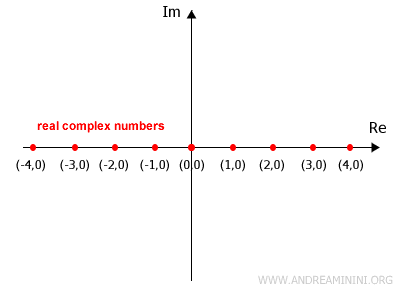
Note. There is a one-to-one correspondence between real complex numbers and real numbers. For every real complex number (a,0), there is a unique real number a, and vice versa. $$ (a,0) \leftrightarrow a $$ In other words, a real complex number and a real number are essentially the same. For example, writing (2,0) is no different from writing 2.

Just like the set of real numbers, the set of real complex numbers is closed under addition and multiplication.

$$ (a,0) + (b,0) = (a + b, 0) $$

$$ (a,0) \cdot (b,0) = (a \cdot b, 0) $$

When you add or multiply two real complex numbers, the result is always another real complex number.

A Practical Example

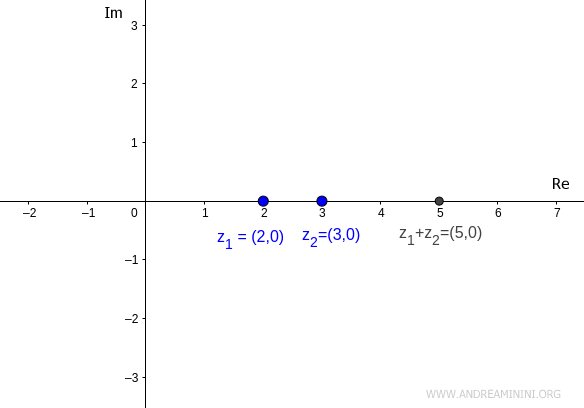
Let’s take two real complex numbers:

$$ z_1 = (2,0) $$

$$ z_2 = (3,0) $$

The sum of these two real complex numbers is also a real complex number because the second component of the pair remains zero.

$$ z_1 + z_2 = (2,0) + (3,0) = (2+3, 0+0) = (5,0) $$

Note. The sum of the real complex numbers (2,0) + (3,0) = (5,0) is identical to the sum of the real numbers 2 + 3 = 5.

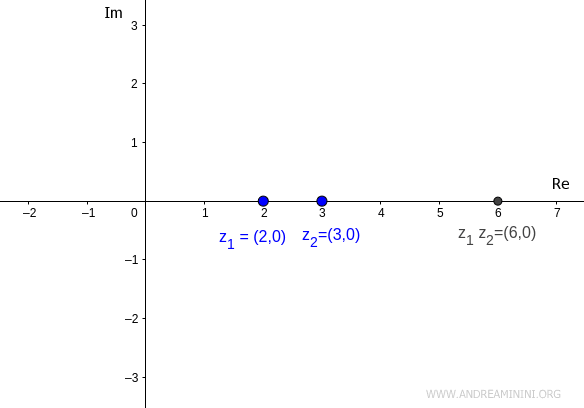
The product of these two real complex numbers is also a real complex number because the second component remains zero.

$$ z_1 \cdot z_2 = (2,0) \cdot (3,0) = (2 \cdot 3 - 0 \cdot 0, 2 \cdot 0 + 0 \cdot 3) = (6,0) $$

Note. The product of the real complex numbers (2,0) · (3,0) = (6,0) is the same as the product of the real numbers 2 · 3 = 6.

And so on.