Polar Representation of Complex Numbers
Complex numbers can also be expressed in polar form.
The polar coordinates of a complex number consist of the modulus r (the length of the vector) and the argument α (the angle) of the directed segment connecting the origin O (pole) to the Cartesian coordinates (x, y) of the complex number z on the Gauss plane.
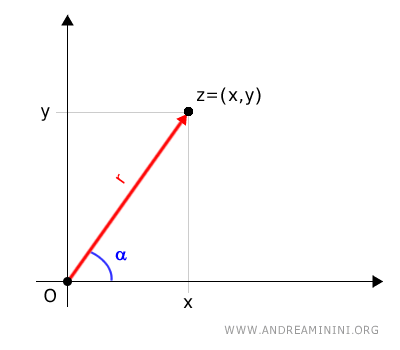
Polar and Cartesian coordinates are simply two different ways of representing a complex number.
How to Find Polar Coordinates
A complex number \( z = x + yi \), which has Cartesian coordinates (x, y) in the Gauss plane, can be written in polar form as \( (r, \alpha) \), where:
$$ r = \sqrt{x^2+y^2} $$
$$ \tan \alpha = \frac{y}{x} $$
Conversely, given the polar coordinates \( (r, \alpha) \), we can find the Cartesian coordinates using:
$$ x = r \cos \alpha $$
$$ y = r \sin \alpha $$
These equations allow us to seamlessly switch between Cartesian and polar forms.
A Practical Example
Consider the complex number \( z = 2 + 3i \).
$$ z = 2 + 3i $$
Its Cartesian coordinates in the Gauss plane are (2,3).
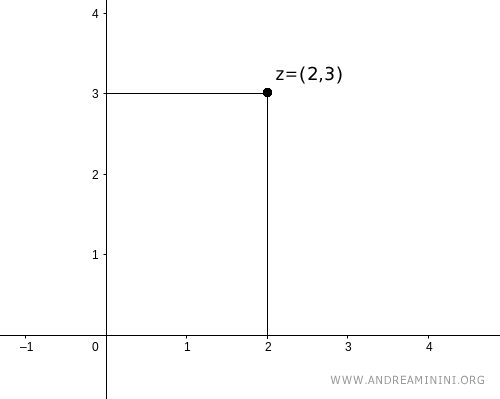
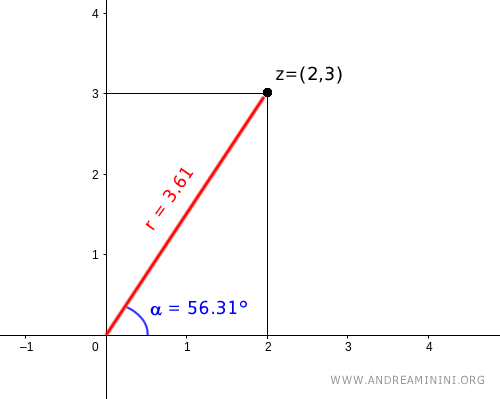
We can also express point P in polar coordinates:
$$ z = P[r, \alpha] $$
Here, \( r = 3.61 \) represents the length of segment OP, while \( \alpha = 56.31^\circ \) is the angle between OP and the positive x-axis.
The Concept Behind It
Every complex number \( z = x + yi \) corresponds to a unique point (x, y) in the Gauss plane.
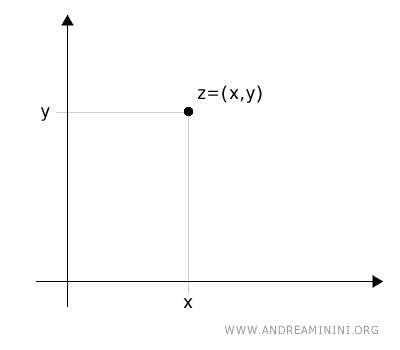
Note: There is a one-to-one correspondence between complex numbers and points on the plane—each complex number corresponds to a unique point, and vice versa.
In this system, the origin (O) serves as the pole, while the positive x-axis is considered the polar axis.
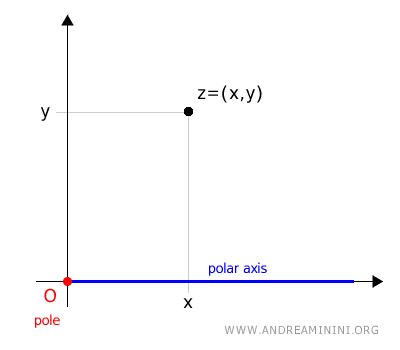
We then draw a directed segment (vector) from the origin to the Cartesian coordinates (a, b) of the complex number.
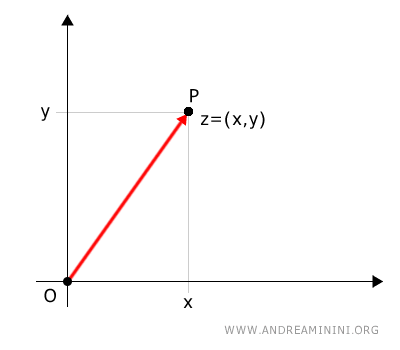
The length of this segment, known as the modulus of the complex number, is denoted by \( r \) (radius).
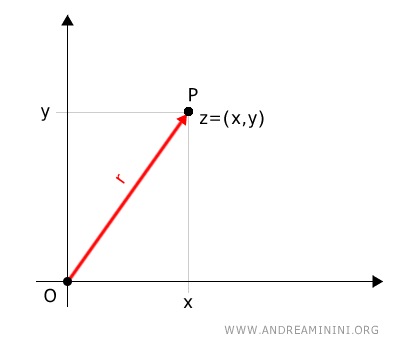
The second polar coordinate is the angle α, measured counterclockwise from the polar axis to the directed segment.
This angle is called the argument of the complex number.
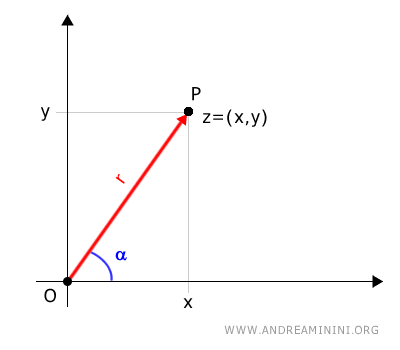
Thus, the polar coordinates of the number are \( P[r,\alpha] \).
Each point in the plane has a unique set of polar coordinates.
Finding the Polar Coordinates of a Complex Number
To convert from Cartesian to polar coordinates, we start with the point (x, y).
$$ z = (x, y) $$
Graphically,
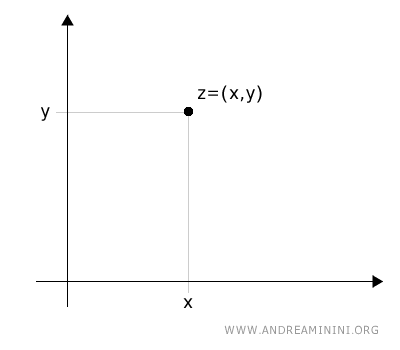
The point (x, y) forms a right triangle OPA in the plane.
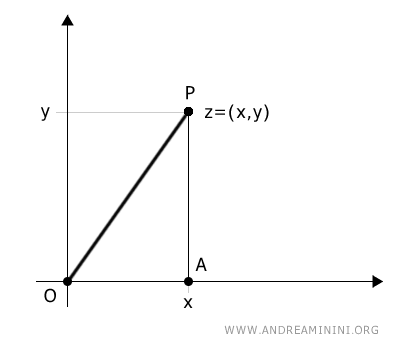
The sides of the triangle are:
$$ \overline{OP} = r, \quad \overline{OA} = x, \quad \overline{AP} = y $$
To find the length of OP, we apply the Pythagorean theorem:
$$ r = \sqrt{x^2+y^2} $$
To determine the angle, we consider the slope of segment OP, given by:
$$ \frac{ y }{ x } = \tan \alpha $$
Applying the arctangent function:
$$ \alpha = \arctan( \frac{ y }{ x } ) $$
Alternative Methods for Finding the Angle: The angle α can also be calculated using inverse trigonometric functions:
Using the cosine function:
$$ x = r \cos \alpha \Rightarrow \alpha = \arccos( \frac{x}{r} ) $$
Using the sine function:
$$ y = r \sin \alpha \Rightarrow \alpha = \arcsin( \frac{y}{r} ) $$
Example
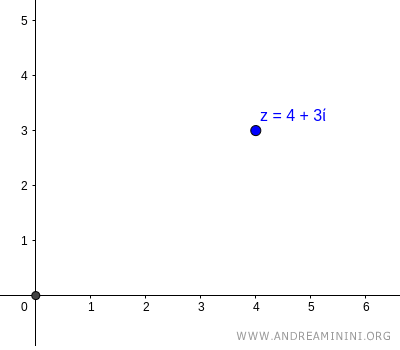
Consider the complex number \( z = 4 + 3i \).
$$ z = 4+3i $$
Its Cartesian coordinates in the Gauss plane are \( (4,3) \), meaning \( x = 4 \) and \( y = 3 \).
To visualize the polar representation, we draw a directed segment (vector) from the origin O (pole) to the point \( (4,3) \).
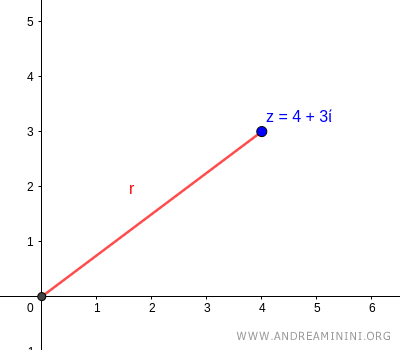
Finding the Modulus
The modulus \( r \) of the complex number is the length of this vector, which we determine using the Pythagorean theorem:
$$ r = \sqrt{x^2 + y^2} $$
Substituting the values:
$$ r = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 $$
Thus, the modulus of the complex number is \( r = 5 \).
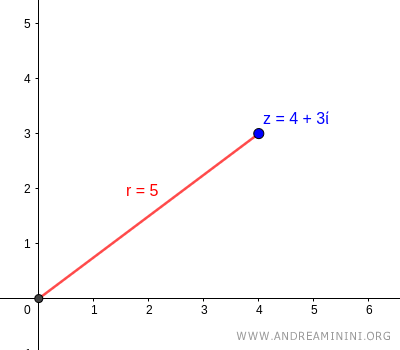
Determining the Argument
The argument \( \alpha \) is the angle between the positive real axis and the vector. It can be found using the arctangent function:
$$ \alpha = \arctan \left( \frac{y}{x} \right) $$
Substituting the given values:
$$ \alpha = \arctan \left( \frac{3}{4} \right) $$
Evaluating:
$$ \alpha \approx 36.87^\circ $$
Thus, the argument of the complex number is \( \alpha \approx 36.87^\circ \).
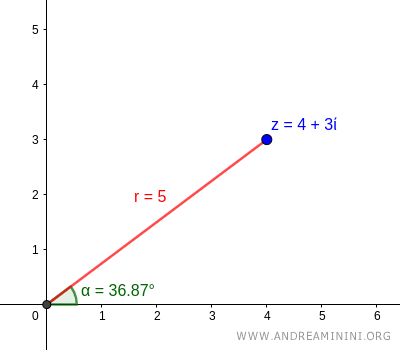
Final Polar Representation
In conclusion, the polar form of the complex number \( z = 4+3i \) is:
$$ P(5, 36.87^\circ) $$
Converting from Polar to Cartesian Coordinates
To convert from polar coordinates \( (r, \alpha) \) back to Cartesian form \( (x, y) \), we use the fundamental trigonometric identities:
$$ x = r \cos \alpha, \quad y = r \sin \alpha $$
The modulus \( r \) and argument \( \alpha \) provide all the necessary information to recover the original Cartesian coordinates.
Example
Let's verify the conversion by taking the polar representation of \( z = 4+3i \):
$$ P(5, 36.87^\circ) $$
Graphically, this corresponds to:
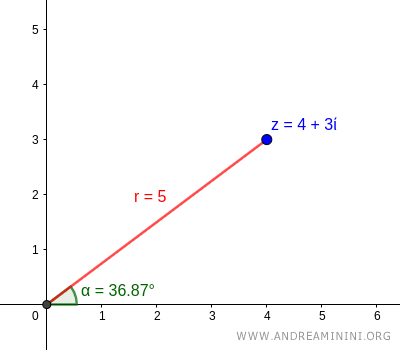
Given:
$$ r = 5, \quad \alpha = 36.87^\circ $$
Applying the conversion formulas:
$$ \begin{cases} x = r \cos \alpha \\ \\ y = r \sin \alpha \end{cases} $$
Substituting \( r = 5 \) and \( \alpha = 36.87^\circ \):
$$ \begin{cases} x = 5 \cos 36.87^\circ \\ \\ y = 5 \sin 36.87^\circ \end{cases} $$
Using the known trigonometric values:
$$ \cos 36.87^\circ \approx 0.8, \quad \sin 36.87^\circ \approx 0.6 $$
We compute:
$$ \begin{cases} x = 5 \times 0.8 = 4 \\ \\ y = 5 \times 0.6 = 3 \end{cases} $$
Final Cartesian Coordinates
Thus, the Cartesian coordinates obtained from the polar form are:
$$ (x, y) = (4, 3) $$
Confirming the accuracy of our calculations.
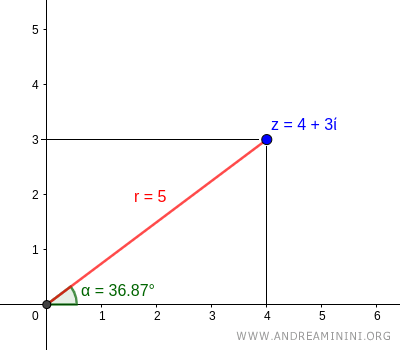
This demonstrates the equivalence between the polar and Cartesian representations of a complex number.
