Complex Conjugate

Two complex numbers are called complex conjugates if they share the same real part (\(a\)) but have imaginary parts (\(b\)) of equal magnitude with opposite signs. $$ z=a+bi $$ $$ z'=a-bi $$

Every complex number has a conjugate, except for \( z = (0,0) \).

If \( a=0 \) and \( b=0 \), the conjugate is undefined.

Complex conjugates vs. opposite numbers. The numbers \( z=2+3i \) and \( z'=2-3i \) are conjugates: $$ z=2+3i \\ z'=2-3i $$ However, the numbers \( z=2+3i \) and \( z'=-2-3i \) are not conjugates because both the real and imaginary parts have opposite signs. In this case, they are known as opposite complex numbers. $$ z=2+3i \\ z'=-2-3i $$ Lastly, the numbers \( z=2+3i \) and \( z'=-2+3i \) are neither conjugates nor opposites, as only the real part has changed sign. $$ z=2+3i \\ z'=-2+3i $$

A Practical Example

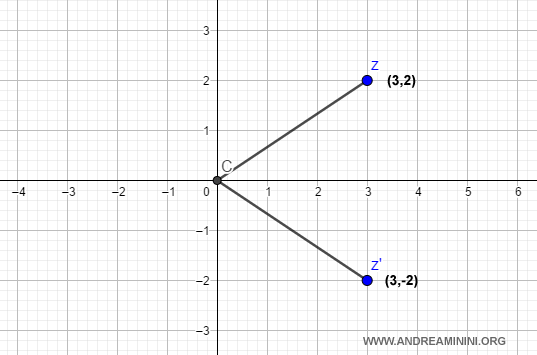
Consider the complex number

$$ z=3+2i $$

Its conjugate is

$$ z'=3-2i $$

Graphically, the conjugate is the reflection of \( z \) across the x-axis.

Properties of Complex Conjugates

Here are some key properties of complex conjugates:

• The sum of a complex number and its conjugate \( z=a+bi \) and \( z'=a-bi \) is a real number: \( 2a \). $$ z+z' = 2a $$

  Proof. Consider a complex number \( z=a+bi \) with both real and imaginary components. Its conjugate is \( z' = a-bi \): $$ z=a+bi \\ z'=a-bi $$ Adding these two numbers: $$ z+z' = (a+bi)+(a-bi) = a+bi+a-bi = 2a $$

• The difference between a complex number and its conjugate \( z=a+bi \) and \( z'=a-bi \) is a purely imaginary number: \( 2bi \). $$ z-z' = 2bi $$

  Proof. Given the conjugate pair \( z=a+bi \) and \( z'=a-bi \): $$ z=a+bi \\ z'=a-bi $$ Their difference is a purely imaginary number, equal to twice the imaginary coefficient of \( z \): $$ z-z' = (a+bi)-(a-bi) $$ $$ z-z' = a+bi-a+bi $$ $$ z-z' = 2bi $$

• The product of a complex number and its conjugate \( z=a+bi \) and \( z'=a-bi \) is always a real number: \( a^2+b^2 \). $$ z \cdot z' = a^2 + b^2 $$

  Proof. Given \( z=a+bi \) and its conjugate \( z'=a-bi \): $$ z=a+bi \\ z'=a-bi $$ Multiplying them: $$ z \cdot z' = (a+bi)\cdot(a-bi) $$ $$ z \cdot z' = a^2-abi+abi-b^2i^2 $$ $$ z \cdot z' = a^2-b^2i^2 $$ Since the square of the imaginary unit is \( i^2=-1 \): $$ z \cdot z' = a^2-b^2(-1) $$ $$ z \cdot z' = a^2+b^2 $$ Therefore, multiplying a complex number by its conjugate always results in the sum of the squares of the real and imaginary components.

And so on.