Complex Exponential Function
The exponential function of a complex number, denoted as \( e^z \), is defined for a complex number \( z = x + iy \), where \( i \) is the imaginary unit.
In general, the complex exponential function can be expressed as an infinite power series:
$$ e^z = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \dots $$
Since \( z = x + iy \) consists of a real part \( x \) and an imaginary part \( iy \), we can rewrite the exponential function as:
$$ e^z = e^{x+iy} $$
Using the property of exponentials that allows the sum of exponents to be split into a product:
$$ e^z = e^{x+iy} = e^x e^{iy} $$
Here, \( e^x \) represents the magnitude (or modulus) of a vector originating at the origin, while the imaginary component \( iy \) determines the argument (angle) of the vector.
By applying Euler's formula:
$$ e^z = e^x e^{iy} = e^x (\cos y + i \sin y) $$
Practical Example
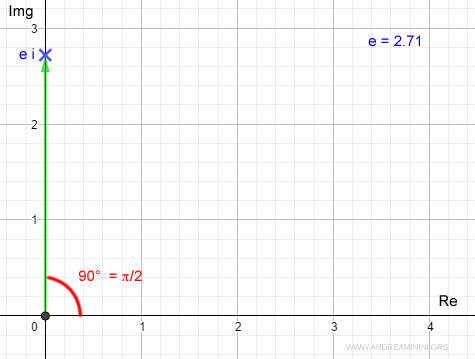
Example 1: Computing a Complex Exponential
Consider the complex exponent:
$$ e^{1+\frac{\pi}{2}i} $$
where \( z = 1 + \frac{\pi}{2}i \).
Here, the real part is \( \text{Re}(z) = 1 \), and the imaginary part is \( \text{Im}(z) = \frac{\pi}{2} \).
We decompose the exponential into its real and imaginary contributions:
$$ e^1 \cdot e^{\frac{\pi}{2} i} $$
Using Euler’s formula, we rewrite the second term in trigonometric form:
$$ e^1 \cdot \left( \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} \right) $$
Since \( \cos \frac{\pi}{2} = 0 \) and \( \sin \frac{\pi}{2} = 1 \), we obtain:
$$ e^1 \cdot (0 + i \cdot 1) $$
Since \( e^1 = e \), we arrive at:
$$ 0 + i e $$
Thus, the complex exponential \( e^z \) for \( z = 1 + \frac{\pi}{2} i \) simplifies to \( i e \).
Example 2: Visualizing the Complex Exponential Function
Now, let's examine the exponential function for a different complex number:
$$ e^{1+2i} $$
Here, the exponent is the complex number \( z = x + yi \), with \( x = 1 \) and \( y = 2 \).
The power series expansion provides a way to approximate the function:
$$ e^z = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \dots $$
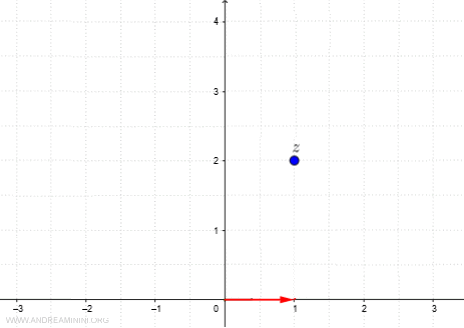
The first term in the series is simply 1, corresponding to \( (1+0i) \).
This means the function starts at the point \( (1,0i) \) in the complex plane.
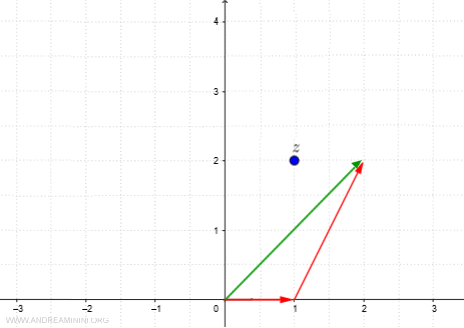
The second term in the expansion is just \( z \), so:
$$ z = 1 + 2i $$
Adding this to the previous result, we obtain:
$$ (1+0i) + (1+2i) = 2 + 2i $$
This defines a new vector from \( (0,0) \) to \( (2,2i) \).
The third term in the expansion involves \( \frac{z^2}{2!} \):
$$ \frac{z^2}{2!} = \frac{(1+2i)^2}{2} = \frac{1 + 4i + 4i^2}{2} = \frac{1 + 4i - 4}{2} = \frac{-3 + 4i}{2} $$
Adding this to our previous sum:
$$ (2+2i) + \frac{-3+4i}{2} $$
Rewriting in a simplified form:
$$ \frac{4 + 4i - 3 + 4i}{2} = \frac{1 + 8i}{2} = \frac{1}{2} + 4i $$
The next vector now extends from \( (0,0) \) to \( \left(\frac{1}{2}, 4i\right) \).
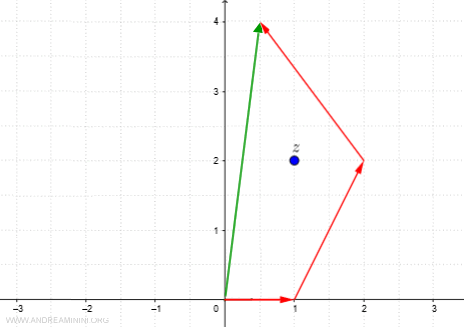
By continuing this process, we approximate the complex exponential function more accurately.
The final result is illustrated below:
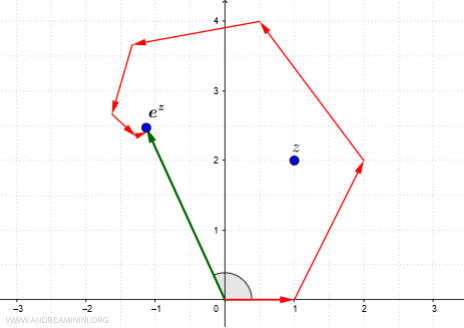
And so on.
