Adding Two Complex Numbers

Adding two complex numbers is simple: just add their real parts together and their imaginary parts together. $$ (a+bi)+(c+di)=(a+c)+(b+d)i $$

In general, the sum of two complex numbers results in another complex number where:

• The real part is the sum of the real parts of both numbers: \( a + c \).
• The imaginary part is the sum of the imaginary coefficients: \( (b + d)i \).

So, the sum of two complex numbers is itself a complex number, where the real part is the sum of the real components, and the imaginary part is the sum of the imaginary coefficients.

A Practical Example

Let's consider two complex numbers:

$$ z_1 = 2 + 3i $$

$$ z_2 = 5 + 2i $$

To add them, we combine their real and imaginary parts:

$$ z_1 + z_2 = (2 + 3i) + (5 + 2i) $$

$$ z_1 + z_2 = (2 + 5) + (3i + 2i) $$

$$ z_1 + z_2 = 7 + 5i $$

So, the sum of these two complex numbers is \( 7 + 5i \).

The Parallelogram Rule

Every complex number can also be represented as a vector on the Gaussian plane.

From a geometric perspective, we can add two complex numbers by summing their corresponding vectors using the parallelogram rule.

A Practical Example

We plot the complex numbers \( z_1 = 2+3i \) and \( z_2 = 5+2i \) on the Gaussian plane.

The first number corresponds to the point (2,3), while the second corresponds to (5,2).

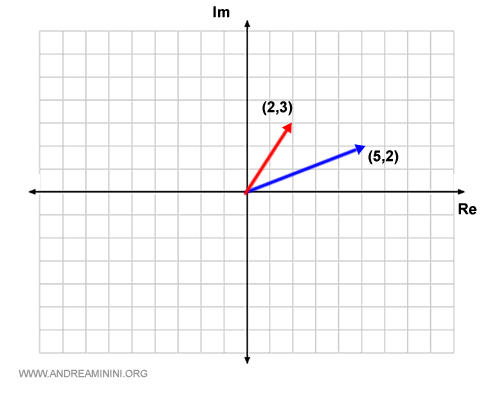
We draw vectors from the origin (0,0) to these points.

Then, we add the two vectors using the parallelogram rule.

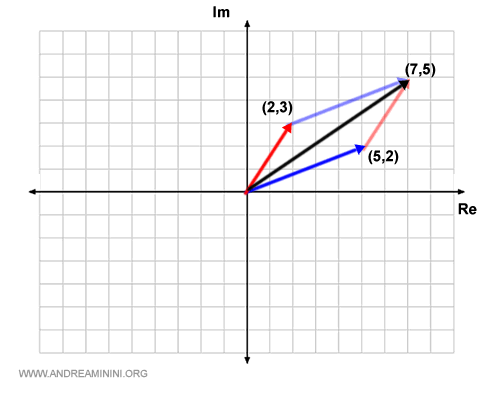
The resulting vector connects the origin to the point (7,5).

This point (7,5) on the Gaussian plane corresponds to the complex number \( 7+5i \).

As expected, this matches the algebraic sum \( z_1 + z_2 \).

Properties of Complex Number Addition

The sum of two complex numbers follows these fundamental properties:

• Commutative Property
  Complex number addition is commutative, meaning that for any two complex numbers \((a, b)\) and \((c, d)\), the order of addition does not matter: $$ (a, b) + (c, d) = (c, d) + (a, b) $$

  Example: Given two complex numbers (1,2) and (3,4), we get: $$ (1,2) + (3,4) = (3,4) + (1,2) = (1+3,2+4) = (4,6) $$

• Associative Property
  Complex number addition is also associative, meaning that for any three complex numbers \((a, b)\), \((c, d)\), and \((e, f)\), the grouping of terms does not affect the result: $$ (a, b) + [(c, d) + (e, f)] = [(a, b) + (c, d)] + (e, f) $$

  Example: Given three complex numbers (1,2), (3,4), and (5,6): $$ (1,2) + (3,4) + (5,6) = (1,2) + [(3,4) + (5,6)] $$

• Identity Element
  The complex number \((0,0)\) acts as the additive identity, meaning that adding it to any complex number leaves the number unchanged: $$ (a, b) + (0, 0) = (a, b) $$

  Example: Given a complex number (1,2): $$ (1,2) + (0,0) = (1,2) $$

• Sum of Numbers of the Form \((a, 0)\)
  The sum of two complex numbers where the imaginary part is zero, i.e., \((a, 0)\) and \((b, 0)\), results in another real number: \((a + b, 0)\). $$ (a,0) + (b,0) = (a+b,0) $$

  Example: Given two complex numbers (1,0) and (3,0): $$ (1,0) + (3,0) = (1+3, 0+0) = (4,0) $$

Proofs

A] Commutative Property of Complex Addition

To prove that complex addition is commutative, let’s consider two arbitrary complex numbers \((a, b)\) and \((c, d)\), where \(a\), \(b\), \(c\), and \(d\) are real numbers.

Their sum is given by:

$$ (a, b) + (c, d) = (a + c, b + d) $$

Now, let’s reverse the order and compute \((c, d) + (a, b)\):

$$ (c, d) + (a, b) = (c + a, d + b) $$

Since addition of real numbers is commutative, we know that \(a + c = c + a\) and \(b + d = d + b\).

Thus, we can rewrite:

$$ (a + c, b + d) = (c + a, d + b) $$

This confirms that:

$$ (a, b) + (c, d) = (c, d) + (a, b) $$

Therefore, complex addition is commutative.

B] Associative Property of Complex Addition

To prove that complex addition is associative, let’s consider three arbitrary complex numbers \((a, b)\), \((c, d)\), and \((e, f)\), where \(a\), \(b\), \(c\), \(d\), \(e\), and \(f\) are real numbers.

We need to show that:

$$ ((a, b) + (c, d)) + (e, f) = (a, b) + ((c, d) + (e, f)) $$

First, we compute the left-hand side:

$$ (a + c, b + d) + (e, f) = ((a + c) + e, (b + d) + f) $$

Next, we compute the right-hand side:

$$ (a, b) + (c + e, d + f) = (a + (c + e), b + (d + f)) $$

Since real number addition is associative, we know that \((a + c) + e = a + (c + e)\) and \((b + d) + f = b + (d + f)\).

Thus, we obtain:

$$ (a + (c + e), (b + d) + f) = (a + (c + e), b + (d + f)) $$

Since both sides are equal, complex addition is associative.

Additional Notes

Here are some useful observations regarding complex number addition:

• Sum of Conjugate Complex Numbers
  The sum of two conjugate complex numbers always results in a real number, which is twice the real part of the original numbers. $$ (a + bi) + (a - bi) = (a + a) + (bi - bi) = 2a $$

  Example: Consider \(3 + 4i\) and its conjugate \(3 - 4i\). Their sum is: $$ (3 + 4i) + (3 - 4i) = 3 + 3 + 4i - 4i = 6 $$ The result is the real number \(6\), which is simply \(2 \times 3\), or twice the real part of the addends.

• Sum of Opposite Complex Numbers
  The sum of two opposite complex numbers is always zero. This is because opposite complex numbers have identical real and imaginary parts in absolute value but with opposite signs, causing them to cancel out. If we take a complex number \(a + bi\), its opposite is \(-(a + bi) = -a - bi\). Their sum is: $$ (a + bi) + (-a - bi) = (a - a) + (b - b)i = 0 + 0i = 0 $$

  Example: Consider the complex number \(5 + 2i\) and its opposite \(-5 - 2i\). Their sum is: $$ (5 + 2i) + (-5 - 2i) = (5 - 5) + (2 - 2)i = 0 + 0i = 0 $$ The result is always \(0\).

And so on.