Root of a Complex Number

To find the n-th root ⁿ√z of a complex number \( z = a + bi \), where \( n \) is a positive integer, we first express it in polar (trigonometric) form: $$ z = d \cdot \left( \cos a + i \sin a \right) $$ Then, we compute its roots using the formula: $$ \sqrt[n]{z} = \sqrt[n]{d} \cdot \left( \cos \frac{a + 2\pi k}{n} + i \sin \frac{a + 2\pi k}{n} \right) $$ for each \( k \) in the range \( 0 \) to \( n-1 \).

The n-th root of \( z \) is a complex number \( w \) such that raising it to the power of \( n \) gives \( z \):

$$ \sqrt[n]{z} = w \Leftrightarrow w^n = z $$

Every nonzero complex number has exactly \( n \) distinct n-th roots.

For instance, a square root yields two solutions, a cube root results in three, and so on.

Computing the n-th Root Using Exponential Form

Alternatively, we can determine the n-th root of a complex number using its exponential representation.

In exponential form, the n-th root ⁿ√z of a complex number is expressed as: $$ \sqrt[n]{z} = d^{\frac{1}{n}} \cdot e^{i \frac{a + 2\pi k}{n} } $$ or more generally: $$ \sqrt[n]{z^m} = d^{\frac{m}{n}} \cdot e^{i m \frac{a + 2\pi k}{n} } $$ where \( n \) is a positive integer (\( n > 0 \)).

Worked Examples

Example 1

Consider the complex number:

$$ z = 3 + i 2 $$

Geometrically, this represents the point \( P(3,2) \) on the complex plane.

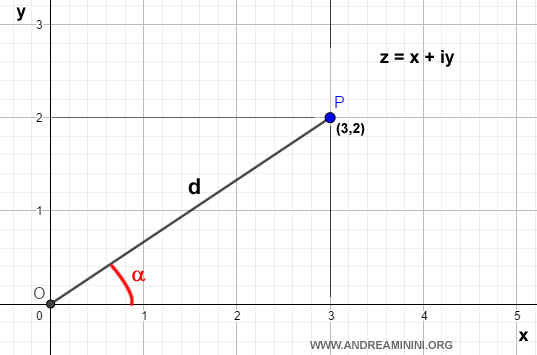
To express \( z \) in trigonometric form, we first compute its modulus:

$$ d = \sqrt{3^2 + 2^2} = \sqrt{13} $$

Thus, we write:

$$ z = \sqrt{13} \left( \cos a + i \sin a \right) $$

To determine the argument \( a \), we use:

$$ \cos a = \frac{x}{d} = \frac{3}{\sqrt{13}} $$

$$ \sin a = \frac{y}{d} = \frac{2}{\sqrt{13}} $$

Using inverse trigonometric functions:

$$ a = \arccos \left( \frac{3}{\sqrt{13}} \right) = 0.588 \text{ rad} $$

$$ a = \arcsin \left( \frac{2}{\sqrt{13}} \right) = 0.588 \text{ rad} $$

Now, let's find the square root (\( n=2 \)) using:

$$ \sqrt[2]{z} = \sqrt[2]{\sqrt{13}} \cdot \left( \cos \frac{a + 2\pi k}{2} + i \sin \frac{a + 2\pi k}{2} \right) $$

Since a square root has two solutions, we evaluate it for \( k=0 \) and \( k=1 \).

For \( k = 0 \):

$$ \sqrt[2]{\sqrt{13}} \cdot \left( \cos \frac{0.588}{2} + i \sin \frac{0.588}{2} \right) $$

$$ \approx 1.817 + i 0.55 $$

For \( k = 1 \):

$$ \sqrt[2]{\sqrt{13}} \cdot \left( \cos \frac{(0.588 + 2\pi)}{2} + i \sin \frac{(0.588 + 2\pi)}{2} \right) $$

$$ \approx -1.817 - i 0.55 $$

Example 2

Now, consider the purely imaginary number:

$$ z = 0 + i 1 $$

or simply:

$$ z = i $$

In polar form, we write:

$$ z = \sqrt{0^2+1^2} \cdot \left( \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} \right) $$

$$ z = 1 \cdot \left( \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} \right) $$

Finding its square roots:

For \( k = 0 \):

$$ \sqrt{z} = \sqrt{1} \cdot \left( \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} \right) $$

$$ = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} $$

For \( k = 1 \):

$$ \sqrt{z} = \sqrt{1} \cdot \left( \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4} \right) $$

$$ = \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4} $$

Proof

Given a complex number:

$$ z = x + iy $$

we express it in polar (trigonometric) form:

$$ z = d \cdot \left( \cos a + i \sin a \right) $$

If \( z' \) is an n-th root of \( z \), then it can also be written in polar form as:

$$ z' = d' \cdot \left( \cos a' + i \sin a' \right) $$

Since \( z' \) is an n-th root, raising it to the power of \( n \) must yield \( z \):

$$ (z')^n = z $$

Substituting the polar forms of \( z \) and \( z' \):

$$ \left( d' \cdot \left( \cos a' + i \sin a' \right) \right)^n = d \cdot \left( \cos a + i \sin a \right) $$

Applying the properties of exponentiation:

$$ (d')^n \cdot \left( \cos a' + i \sin a' \right)^n = d \cdot \left( \cos a + i \sin a \right) $$

From this, it follows that \( d' \) must be the n-th root of \( d \):

$$ d' = \sqrt[n]{d} $$

Substituting this into our equation:

$$ \sqrt[n]{d} \cdot \left( \cos a' + i \sin a' \right)^n = d \cdot \left( \cos a + i \sin a \right) $$

Since the cosine and sine functions are periodic with period \( 2\pi \), we account for all possible angles by writing:

$$ \sqrt[n]{d} \cdot \left( \cos a' + i \sin a' \right)^n = d \cdot \left( \cos (a + 2\pi k) + i \sin (a + 2\pi k) \right) $$

Applying De Moivre’s Theorem on complex number exponentiation, we expand the left-hand side:

$$ \sqrt[n]{d} \cdot \left( \cos (n a') + i \sin (n a') \right) = d \cdot \left( \cos (a + 2\pi k) + i \sin (a + 2\pi k) \right) $$

Explanation: To see why this works, consider the special case where \( n = 2 \). We expand:

$$ (\cos a + i \sin a)^2 $$

Using the binomial expansion:

$$ \cos^2 a + 2i \cos a \sin a + i^2 \sin^2 a $$

Since \( i^2 = -1 \), this simplifies to:

$$ \cos^2 a + 2i \cos a \sin a - \sin^2 a $$

Using trigonometric double-angle identities:

$$ \cos^2 a - \sin^2 a = \cos 2a $$

$$ 2 \sin a \cos a = \sin 2a $$

So we obtain:

$$ \cos 2a + i \sin 2a $$

Comparing both sides of the equation, we deduce that:

$$ n a' = a + 2\pi k $$

Solving for \( a' \):

$$ a' = \frac{a + 2\pi k}{n} $$

Thus, for any complex number \( z \), expressed in polar form as:

$$ z = d \cdot \left( \cos a + i \sin a \right) $$

if \( z' \) is an n-th root of \( z \), we have:

$$ z' = \sqrt[n]{z} $$

which means:

$$ d' \cdot \left( \cos a' + i \sin a' \right) = \sqrt[n]{z} $$

Substituting our previously found expressions for \( d' \) and \( a' \):

$$ \sqrt[n]{d} \cdot \left( \cos \frac{a + 2\pi k}{n} + i \sin \frac{a + 2\pi k}{n} \right) = \sqrt[n]{z} $$

This is precisely the formula we set out to prove.

An Alternative Method for Computing Roots

Once we have found the first n-th root of a complex number, we can derive the remaining roots by multiplying this solution by the n-th roots of unity.

The general formula for obtaining all n-th roots is:

$$ \sqrt[n]{d} \cdot \left( \cos \frac{\alpha}{n} + i \sin \frac{\alpha}{n} \right) \cdot \sqrt[n]{1} $$

Since the n-th roots of unity satisfy:

$$ \sqrt[n]{1} = \cos \frac{2k\pi}{n} + i \sin \frac{2k\pi}{n}, \quad k = 0,1,\dots, n-1 $$

we can rewrite the formula as:

$$ \sqrt[n]{d} \cdot \left( \cos \frac{\alpha}{n} + i \sin \frac{\alpha}{n} \right) \cdot \left( \cos \frac{2k\pi}{n} + i \sin \frac{2k\pi}{n} \right) $$

Example: Finding the Square Roots of \( i \)

Let's revisit the complex number:

$$ z = 0 + i $$

In polar form, this is:

$$ z = 1 \cdot \left( \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} \right) $$

Since we are computing the square roots (\( n = 2 \)), there are two solutions.

The principal root (for \( k = 0 \)) is:

$$ \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} $$

Note: This result was derived in the previous example. For reference, the derivation follows:

$$ \sqrt{z} = \sqrt{1} \cdot \left( \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} \right) $$

Computing the Second Root Using Roots of Unity

Rather than repeating the full calculation for \( k = 1 \), we use the fact that the second root can be found by multiplying the principal root by the square root of unity.

$$ \left( \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} \right) \cdot \left( \cos \frac{2k\pi}{n} + i \sin \frac{2k\pi}{n} \right) $$

Substituting \( k = 1 \) and \( n = 2 \):

$$ \left( \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} \right) \cdot \left( \cos \pi + i \sin \pi \right) $$

Using the multiplication formula for complex numbers in polar form, we apply angle addition:

$$ \cos \left( \frac{\pi}{4} + \pi \right) + i \sin \left( \frac{\pi}{4} + \pi \right) $$

Since \( n = 2 \), we compute:

$$ \cos \left( \frac{\pi}{4} + \frac{2\pi}{2} \right) + i \sin \left( \frac{\pi}{4} + \frac{2\pi}{2} \right) $$

$$ \cos \left( \frac{\pi + 4\pi}{4} \right) + i \sin \left( \frac{\pi + 4\pi}{4} \right) $$

$$ \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4} $$

This result is identical to the one obtained using direct computation.

Verification

To confirm our approach, we compare it with the explicit calculation for \( k = 1 \) from the previous example:

$$ \sqrt{z} = \sqrt{1} \cdot \left( \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4} \right) $$

which simplifies to:

$$ \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4} $$

Thus, the alternative method gives the same result as direct computation.

Generalizing the Method

This approach provides an efficient way to compute all n-th roots of a complex number:

• First, compute the principal root (for \( k = 0 \)).
• Then, obtain the remaining roots by multiplying the principal root by successive n-th roots of unity.

This avoids redundant calculations and provides a structured method for finding all n-th roots of any complex number.