Multiplication of Two Complex Numbers in Exponential Form

The product of two complex numbers in exponential form is another complex number whose modulus is the product of the moduli, and whose argument is the sum of the arguments. This follows directly from the properties of exponentials: $$ z_1 \cdot z_2 = (r_1 \cdot r_2) \cdot e^{i(\alpha + \beta)} $$

A Practical Example

Let’s take two complex numbers:

$$ z_1 = 1 + 3i $$

$$ z_2 = 4 + 2i $$

On the complex plane (also known as the Argand plane), these correspond to the points \( (1,3) \) and \( (4,2) \).

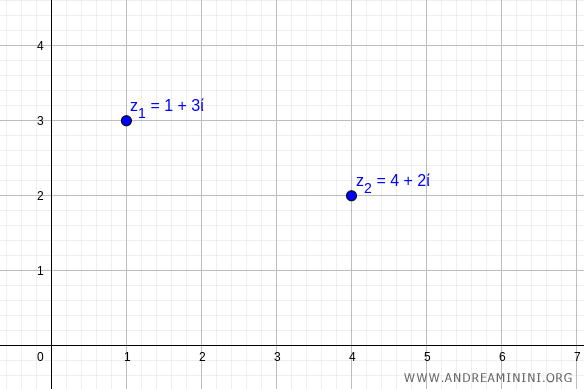
Now, let’s convert these numbers into their trigonometric form.

Step 1: Compute the Moduli

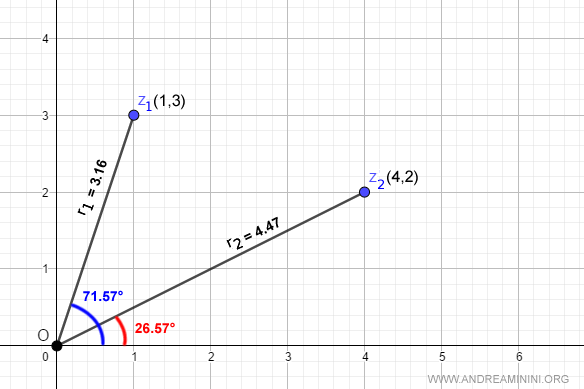
The modulus (or absolute value) of a complex number \( z = x + yi \) is given by \( r = \sqrt{x^2 + y^2} \). Applying this to our numbers:

$$ r_1 = \sqrt{1^2+3^2} = \sqrt{10} \approx 3.16 $$

$$ r_2 = \sqrt{4^2+2^2} = \sqrt{20} \approx 4.47 $$

Step 2: Compute the Arguments

The argument of a complex number is the angle \( \theta \) it makes with the positive real axis, given by \( \theta = \arctan(y/x) \):

$$ \alpha = \arctan \frac{3}{1} = 71.57^\circ $$

$$ \beta = \arctan \frac{2}{4} = 26.57^\circ $$

Thus, the two numbers in trigonometric form are:

$$ z_1 = 3.16 \cdot ( \cos 71.57^\circ + i \sin 71.57^\circ ) $$

$$ z_2 = 4.47 \cdot ( \cos 26.57^\circ + i \sin 26.57^\circ ) $$

In polar coordinates \([r, \alpha]\), these represent the same complex numbers, just expressed differently.

Step 3: Convert to Exponential Form

Using Euler’s formula, \( e^{i\theta} = \cos\theta + i\sin\theta \), we express the numbers in exponential form:

$$ z_1 = 3.16 \cdot e^{i 71.57^\circ} $$

$$ z_2 = 4.47 \cdot e^{i 26.57^\circ} $$

Step 4: Multiply the Two Numbers

Now, we apply the multiplication rule for complex numbers in exponential form:

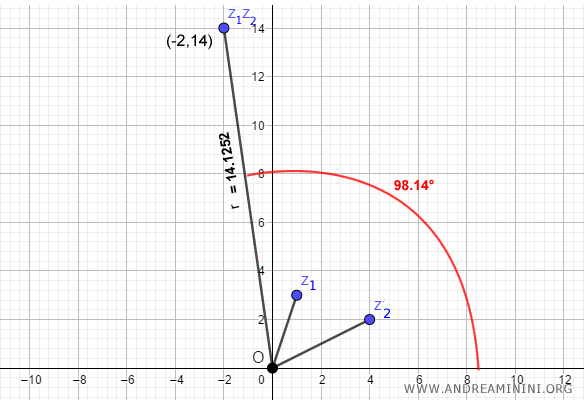
$$ z_1 \cdot z_2 = (3.16 \cdot 4.47) \cdot e^{i (71.57^\circ + 26.57^\circ)} $$

$$ z_1 \cdot z_2 = 14.1252 \cdot e^{i 98.14^\circ} $$

Step 5: Convert Back to Trigonometric Form

Rewriting the result in trigonometric form:

$$ z_1 \cdot z_2 = 14.1252 \cdot ( \cos 98.14^\circ + i \sin 98.14^\circ ) $$

Step 6: Convert to Algebraic Form

Now, we compute the sine and cosine values to express the result in standard algebraic form:

$$ z_1 \cdot z_2 = 14.1252 \cdot \cos 98.14^\circ + 14.1252 \cdot i \sin 98.14^\circ $$

$$ z_1 \cdot z_2 = -2 + 14i $$

Thus, the product of the two complex numbers is \( -2 + 14i \).

Verification

Checking the Result: To confirm our result, let's recompute the product directly in algebraic form:

$$ z_1 \cdot z_2 = (1+3i) \cdot (4+2i) $$

$$ z_1 \cdot z_2 = 4 + 2i + 12i + 6i^2 $$

Since \( i^2 = -1 \), we simplify:

$$ z_1 \cdot z_2 = 4 + 14i + 6(-1) $$

$$ z_1 \cdot z_2 = -2 + 14i $$

As expected, the result is the same.

And that’s it!