Gauss's Plane

The Gauss plane (also known as the complex plane) is a Cartesian coordinate system (Oxy) used to represent complex numbers. The x-axis is referred to as the real axis (Re), while the y-axis is called the imaginary axis (Im).
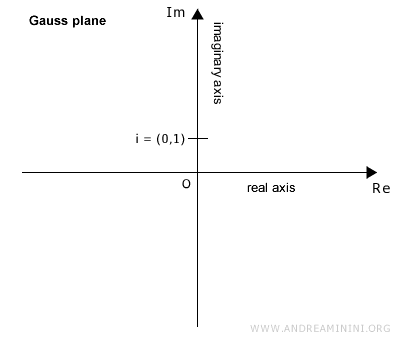
the Gauss plane or complex plane
The symbol i represents the imaginary unit, located at the coordinates (0,1).

Every complex number is represented as an ordered pair (a, b) of real numbers.

$$ z = (a, b) $$

Thus, there is a one-to-one correspondence between complex numbers and points in the Cartesian plane (x, y).

Each complex number corresponds uniquely to a point in the plane, and vice versa.

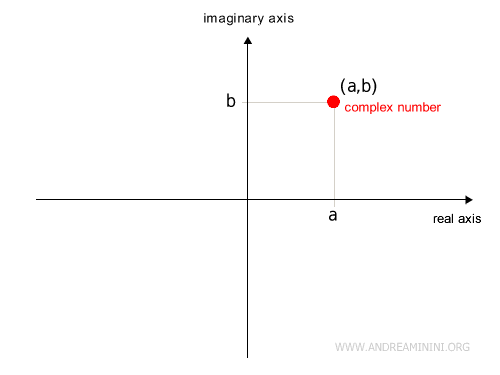
the relationship between complex numbers and points in the plane

On the x-axis, real numbers are plotted, while imaginary numbers are measured along the y-axis.

This allows the Cartesian plane to geometrically represent complex numbers, where each point is composed of a real part and an imaginary part.

This type of diagram is called the complex plane or the Gauss plane.

Since there is a one-to-one correspondence between points in the plane and vectors, it follows that every complex number can be represented as a vector $ \vec{v} $ with components (a, b), and vice versa.

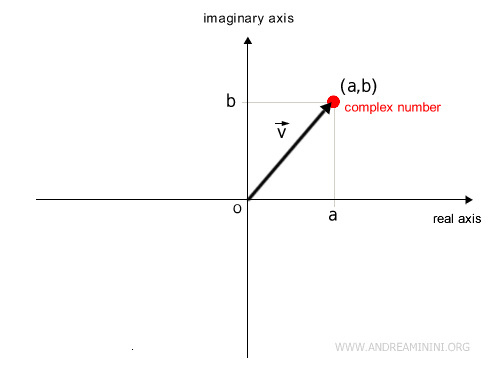
a complex number represented geometrically as a vector

In other words, each complex number $ a + bi $ corresponds to one and only one vector $ \vec{v} $ in $ \mathbb{R}^2 $, and vice versa.

$$ a + bi \Longleftrightarrow \vec{v} = \begin{pmatrix} a \\ b \end{pmatrix} $$

This principle forms the basis of the polar representation of complex numbers.

the polar representation of complex numbers

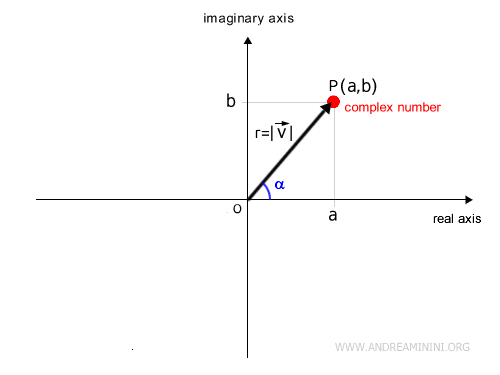
In the polar coordinate system, any complex number $ z = a + bi $ is represented by a pair of values (r, α):

The modulus (r), which represents the length of the vector $ \vec{v} $ from the origin O (the "pole") of the Gauss plane to the point P(a, b).
The argument (α), which is the angle (measured counterclockwise) between the vector and the positive x-axis of the Gauss plane (the polar axis).

Note: In the polar coordinate system, the origin O of the Gauss plane (the pole) has coordinates (0, α), where α can represent any angle. However, since the angle α is equivalent to infinitely many angles of the form $ \alpha + 2k\pi $ (by adding k full rotations, $ 2\pi = 360^\circ $), the principal argument is typically defined as the angle within the range $ 0 \leq \alpha < 2\pi $.

A Practical Example

Consider the complex number $ z = 2 + 3i $.

$$ z = 2 + 3i $$

The real part of the complex number is 2, while the coefficient of the imaginary part is 3.

Therefore, the complex number corresponds to the coordinates (2, 3) in the Gauss plane.

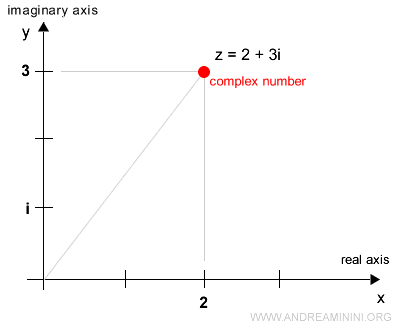
practical example of a complex number

There is a one-to-one correspondence between the point (2, 3) and the complex number $ z = 2 + 3i $.

Proof: The point (2, 3) can be expressed as the sum of a real number (2, 0) and an imaginary number (0, 3): $$ (2, 3) = (2, 0) + (0, 3) $$ Since any imaginary number is the product of the imaginary unit and a real number, $ (0, 3) $ can be rewritten as $ (0, 1) \cdot (3, 0) $: $$ (2, 3) = (2, 0) + [(0, 1) \cdot (3, 0)] $$ Let $ i = (0, 1) $, the imaginary unit: $$ (2, 3) = (2, 0) + [i \cdot (3, 0)] $$ Both $ (2, 0) $ and $ (3, 0) $ are real numbers, where $ (2, 0) = 2 $ and $ (3, 0) = 3 $. $$ (2, 3) = 2 + 3i $$ This result gives the complex number $ z = 2 + 3i $ in algebraic form.

And so on.