Euler’s Formulas

Euler’s formula establishes a deep and elegant connection between trigonometric functions and the complex exponential function: $$ e^{ix} = \cos x + i \sin x $$ where \( x \) is a real number (expressed in radians), \( e \) is the base of natural logarithms, and \( i \) is the imaginary unit in complex numbers.

What is it used for?

Euler’s formula allows us to express complex numbers in exponential form:

$$ z = d \cdot e^{ix} = d \cdot ( \cos x + i \sin x ) $$

Here, \( d \) represents the modulus (absolute value of \( z \)), and \( x \) is the argument of the complex number, measured in radians.

By rewriting complex numbers in this form, we can leverage the exponential function \( e^x \) instead of trigonometric functions, streamlining many mathematical operations.

For example, the multiplication of two complex numbers in exponential form follows the familiar exponentiation rules: $$ z_1 \cdot z_2 = ( r_1 e^{i \alpha } ) \cdot ( r_2 e^{i \beta} ) = ( r_1 \cdot r_2 ) e^{i(\alpha+\beta)} $$ Likewise, division of complex numbers is just as straightforward: $$ \frac{z_1}{z_2} = \frac{r_1 e^{i \alpha }}{r_2 e^{i \beta}} = \left( \frac{r_1}{r_2} \right) e^{i(\alpha-\beta)} $$

From Euler’s fundamental equation, we can derive three other key formulas that play a crucial role in scientific and engineering applications.

Key Derived Formulas

Complex Conjugate

$$ e^{-ix} = \cos x - i \sin x $$

Cosine Expression

$$ \cos x = \frac{e^{ix} + e^{-ix}}{2} $$

Sine Expression

$$ \sin x = \frac{e^{ix} - e^{-ix}}{2i} $$

These four expressions collectively make up what are known as Euler’s formulas.

Example: Consider the complex number $$ z = 1 + 3i $$ Its exponential form is given by $$ z = \sqrt{10} \cdot e^{i \cdot 71.57^\circ} $$ where \( d = \sqrt{10} \) is the modulus and \( x = 71.57^\circ \) is the argument. To find the complex conjugate \( z' = 1 - 3i \) in exponential form, we simply negate the exponent: $$ z' = \sqrt{10} \cdot e^{-i \cdot 71.57^\circ} $$ Once we have \( z \) and \( z' \), Euler’s formulas allow us to quickly compute the cosine and sine of the argument \( x \).

Geometric Interpretation

The argument \( x \) represents the angle of a vector that extends from the origin of the complex plane to a point on the unit circle.

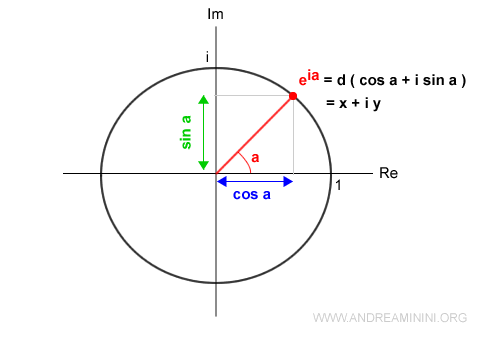
The length of this vector corresponds to the modulus of the complex number, while the angle \( x \) (measured counterclockwise from the positive real axis) is the argument.

Together, the modulus and argument \([d; x]\) define the polar coordinates of the complex number.

These are the same polar coordinates used in the trigonometric form of a complex number:

$$ d \cdot e^{ix} = d \cdot ( \cos x + i \sin x ) $$

Thus, Euler’s formula provides an elegant and powerful way to represent complex numbers in exponential form, making many mathematical operations more intuitive and efficient.

Proof

Euler’s formula is the foundation for several other key identities that are widely used in mathematics and scientific computations.

The Complex Conjugate

The complex conjugate of a number expressed in exponential form, \( z = e^{ix} \), is obtained simply by negating the exponent:

$$ e^{-ix} = \cos x - i \sin x $$

Proof. A complex number can be expressed in algebraic, trigonometric, and exponential forms: $$ z = a+bi = d ( \cos x + i \sin x ) = d \cdot e^{ix} $$ The complex conjugate maintains the same modulus but negates the imaginary part: $$ z' = a - bi = d ( \cos x - i \sin x ) $$ Thus, in exponential form, the conjugate is simply: $$ z' = d e^{-ix} $$ which confirms the result.

The Cosine Identity

$$ \cos x = \frac{e^{ix} + e^{-ix}}{2} $$

Proof. Consider a complex number \( z \) and its conjugate \( z' \): $$ z = \cos x + i \sin x = e^{ix} $$ $$ z' = \cos x - i \sin x = e^{-ix} $$ Adding both equations: $$ ( \cos x + i \sin x ) + ( \cos x - i \sin x ) = e^{ix} + e^{-ix} $$ Since the imaginary terms cancel out: $$ 2 \cos x = e^{ix} + e^{-ix} $$ Solving for \( \cos x \): $$ \cos x = \frac{e^{ix} + e^{-ix}}{2} $$ which is the identity we wanted to prove.

The Sine Identity

$$ \sin x = \frac{e^{ix} - e^{-ix}}{2i} $$

Proof. Using \( z \) and \( z' \) once again: $$ z = \cos x + i \sin x = e^{ix} $$ $$ z' = \cos x - i \sin x = e^{-ix} $$ Subtracting the second equation from the first: $$ ( \cos x + i \sin x ) - ( \cos x - i \sin x ) = e^{ix} - e^{-ix} $$ This time, the cosine terms cancel out, leaving: $$ 2 i \sin x = e^{ix} - e^{-ix} $$ Solving for \( \sin x \): $$ \sin x = \frac{e^{ix} - e^{-ix}}{2i} $$ which completes the proof.

Key Observations

A few important notes on Euler’s formulas:

• When the angle is \( 180^\circ \), or \( \alpha = \pi \) radians, Euler’s formula reduces to: $$ e^{\pi i} + 1 = 0 $$ This is one of the most famous equations in mathematics, as it elegantly ties together five fundamental mathematical constants: \( 1 \), \( 0 \), \( e \), \( i \), and \( \pi \).

  Proof. Setting \( \alpha = \pi \) in Euler’s formula: $$ e^{i \pi} = \cos \pi + i \sin \pi $$ Since \( \cos \pi = -1 \) and \( \sin \pi = 0 \), this simplifies to: $$ e^{i \pi} = -1 + i \cdot 0 $$ $$ e^{i \pi} = -1 $$ Adding 1 to both sides: $$ e^{i \pi} + 1 = 0 $$

And so on.