Trigonometric Form of Complex Numbers

A complex number \( z = a + bi \) can also be expressed in trigonometric form as: $$ z = r \cdot [\cos(\alpha) + i \sin(\alpha)] $$

Here, \( r \) represents the modulus (or magnitude), while \( \alpha \) is the argument, which corresponds to the angle in the polar coordinate representation of the complex number \( z = a + bi \) on the complex plane.

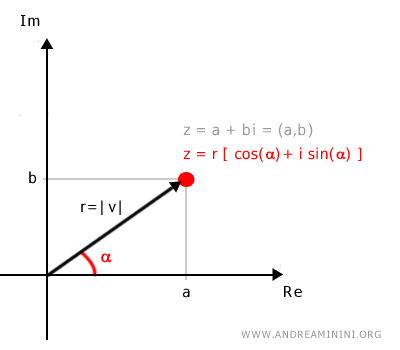
For this reason, the trigonometric form of \( z = a + bi \) is also referred to as the polar form of a complex number.

Finding the Modulus and Argument

The modulus \( r \) is given by the Pythagorean theorem:

$$ r = \sqrt{a^2 + b^2} $$

The argument \( \alpha \) (also called the phase angle) is found using the inverse tangent function:

$$ \tan \alpha = \frac{b}{a} \Longrightarrow \alpha = \arctan \frac{b}{a} $$

Why use the trigonometric form? Expressing complex numbers in trigonometric form simplifies operations such as multiplication, division, exponentiation, and finding roots. These operations become much more intuitive when working with angles and magnitudes rather than real and imaginary components.

A Practical Example

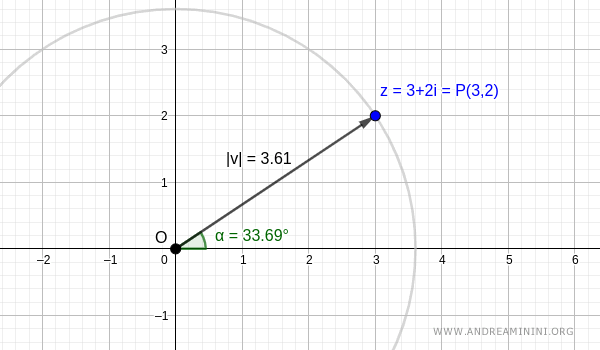
Consider the complex number:

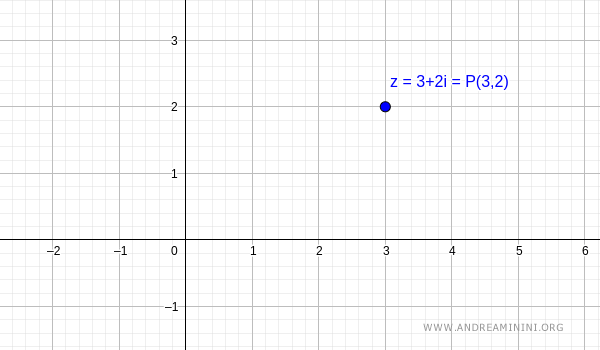
$$ z = 3 + 2i $$

This corresponds to the point \( P \) with Cartesian coordinates \( (x, y) = (3,2) \) on the complex plane (also called the Argand diagram).

Alternatively, the same complex number can be visualized as a vector \( v \), which extends from the origin \( O \) to the point \( P(3,2) \).

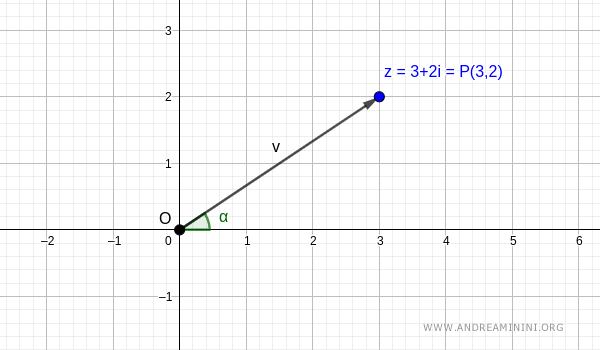
Note: The vector has a length (modulus) denoted as \( |v| \) and an angle (argument) \( \alpha \). We haven’t computed them yet, but they can be easily determined using polar coordinates.

Converting to Trigonometric Form

To obtain the trigonometric form, we first determine the modulus \( r \) and argument \( \alpha \).

We construct a circle centered at \( O \) with radius \( r = |v| \), passing through \( P(3,2) \).

The projections of \( P \) onto the coordinate axes correspond to the Cartesian components of \( z = 3 + 2i \), meaning \( x = 3 \) and \( y = 2 \).

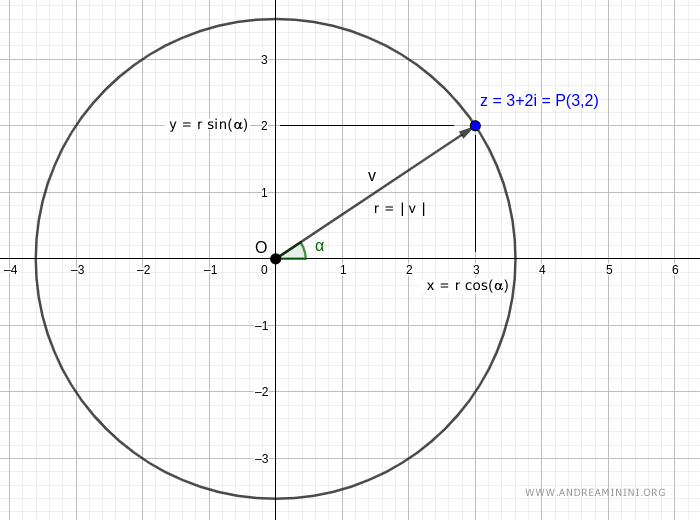
From trigonometry, we know that:

\( x = r \cos(\alpha) \) and \( y = r \sin(\alpha) \).

Substituting these into our complex number equation:

$$ z = x + yi = 3 + 2i $$

$$ z = (r \cos \alpha) + (r \sin \alpha) i $$

Factoring out \( r \), we obtain the trigonometric form:

$$ z = r \cdot (\cos \alpha + i \sin \alpha) $$

Computing the Modulus and Argument

The modulus \( r \) is given by:

$$ r = \sqrt{x^2 + y^2} = \sqrt{3^2 + 2^2} = \sqrt{13} \approx 3.61 $$

The argument \( \alpha \) is computed as:

$$ \alpha = \arctan \frac{y}{x} = \arctan \frac{2}{3} \approx 33.69^\circ $$

Explanation: Using the fundamental trigonometric identity:

$$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} $$

Since we know \( x = r \cos \alpha \) and \( y = r \sin \alpha \), we get:

$$ \tan \alpha = \frac{y}{x} $$

Taking the inverse tangent:

$$ \alpha = \arctan \left(\frac{y}{x}\right) $$

Thus, the polar coordinates of \( P \) are:

$$ P:[r ; \alpha] = [ \sqrt{13} , 33.69^\circ ] $$

which correspond to the modulus \( r \) and argument \( \alpha \) of the complex number in trigonometric form.

Final Trigonometric Representation

Substituting our values:

$$ z = \sqrt{13} \cdot (\cos 33.69^\circ + i \sin 33.69^\circ) $$

Graphically, this representation looks like:

Proof

There is a one-to-one correspondence between complex numbers and points on the plane.

Each complex number \( z = a + bi \) corresponds uniquely to a point with Cartesian coordinates \( (a, b) \), and vice versa.

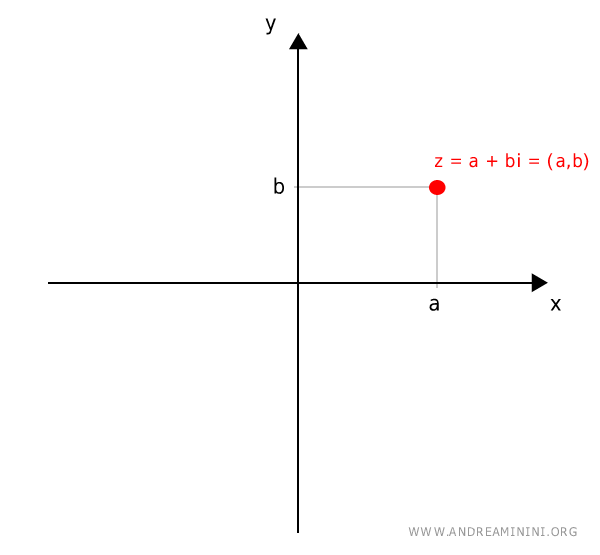
A point with Cartesian coordinates \( (a, b) \) can also be expressed using polar coordinates, denoted as \([r, \alpha]\).

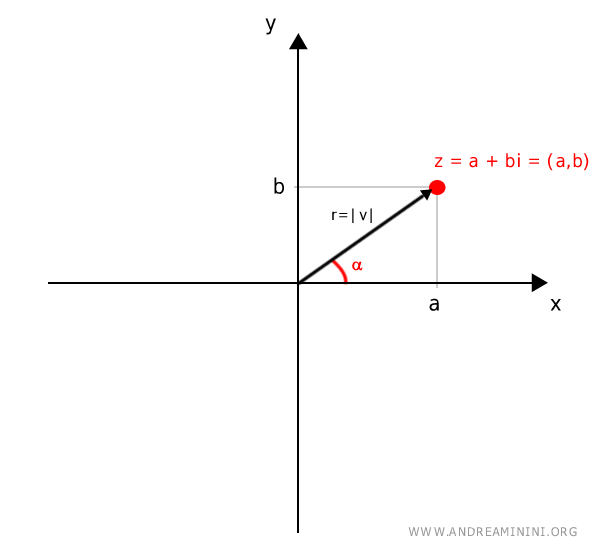
Polar coordinates consist of two components:

• The modulus (\( r \))
  The modulus represents the magnitude of the complex number, which corresponds to the length of the vector \( |v| \) connecting the origin (pole) to the point \( P \).
• The argument (\( \alpha \))
  The argument is the angle \( \alpha \) that the vector \( v \) makes with the positive real axis.

To visualize this, we draw a circle centered at \( O \) with radius \( r = |v| \) passing through the point \( (a, b) \).

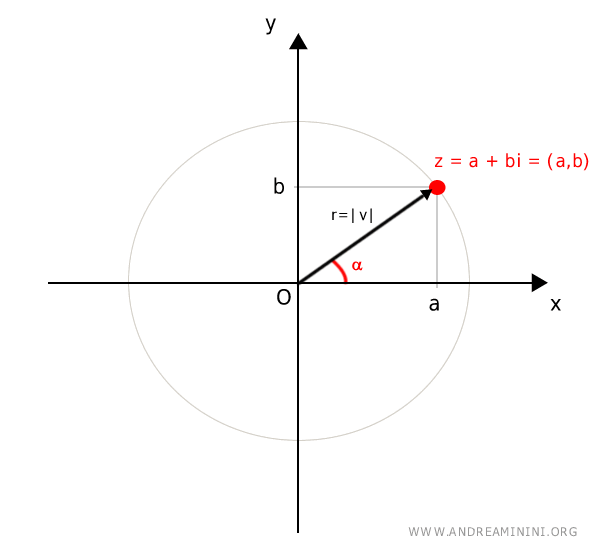
The projections of point \( (a, b) \) onto the coordinate axes correspond to the real and imaginary components of the complex number \( z = a + bi \):

$$ z = a + bi $$

From trigonometry, the coordinates \( a \) and \( b \) can be expressed in terms of \( r \) and \( \alpha \) as follows:

$$ a = r \cos \alpha $$

$$ b = r \sin \alpha $$

Graphically:

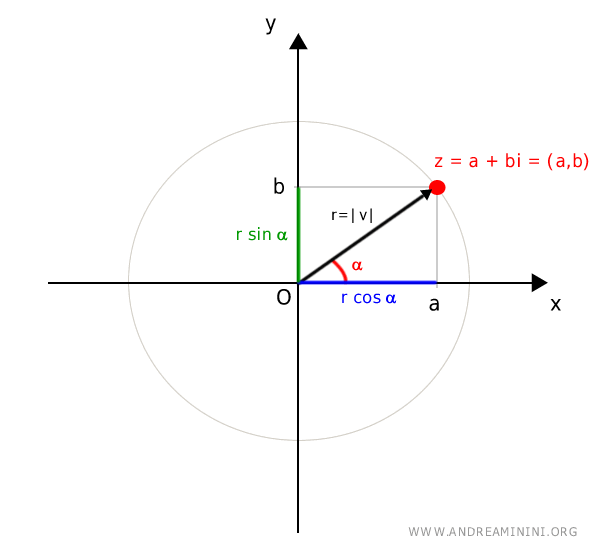
Substituting \( a = r \cos \alpha \) and \( b = r \sin \alpha \) into the expression for \( z \):

$$ z = a + bi $$

$$ z = (r \cos \alpha) + (r \sin \alpha) i $$

Factoring out \( r \), we obtain the trigonometric form of the complex number:

$$ z = r \cdot (\cos \alpha + i \sin \alpha) $$

Deriving the Modulus and Argument

The modulus \( r \) is given by the Pythagorean theorem:

$$ r = \sqrt{a^2 + b^2} $$

The argument \( \alpha \) is found using the inverse tangent function:

$$ \alpha = \arctan \frac{b}{a} $$

Note: According to a fundamental trigonometric identity, the ratio of sine to cosine for a given angle is equal to its tangent: $$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} $$ Since we know that \( a = r \cos \alpha \) and \( b = r \sin \alpha \), we can express cosine and sine as: \( \cos \alpha = \frac{a}{r} \) and \( \sin \alpha = \frac{b}{r} \). Substituting these into the tangent definition: $$ \tan \alpha = \frac{ \frac{b}{r} }{ \frac{a}{r} } $$ $$ \tan \alpha = \frac{b}{r} \cdot \frac{r}{a} $$ $$ \tan \alpha = \frac{b}{a} $$ Applying the arctangent function to both sides: $$ \arctan( \tan \alpha) = \arctan( \frac{b}{a} ) $$ $$ \alpha = \arctan( \frac{b}{a} ) $$ This gives the argument \( \alpha \) of the complex number.

Alternative Methods for Finding the Argument

Instead of using the arctangent, the argument \( \alpha \) can also be determined using the arccosine function:

$$ \alpha = \arccos{\frac{a}{r}} $$

Since \( r = \sqrt{a^2 + b^2} \), we rewrite it as:

$$ \alpha = \arccos{\frac{a}{\sqrt{a^2+b^2}}} $$

Note: Since $$ a = r \cos \alpha $$ we can express cosine as: $$ \cos \alpha = \frac{a}{r} $$ Applying the inverse cosine function to both sides: $$ \arccos( \cos \alpha ) = \arccos( \frac{a}{r} ) $$ $$ \alpha = \arccos( \frac{a}{r} ) $$

Similarly, the argument can be found using the arcsine function:

$$ \alpha = \arcsin{\frac{b}{r}} $$

Since \( r = \sqrt{a^2 + b^2} \), we rewrite it as:

$$ \alpha = \arcsin{\frac{b}{\sqrt{a^2+b^2}}} $$

Note: Since $$ b = r \sin \alpha $$ we can express sine as: $$ \sin \alpha = \frac{b}{r} $$ Applying the inverse sine function to both sides: $$ \arcsin( \sin \alpha ) = \arcsin( \frac{b}{r} ) $$ $$ \alpha = \arcsin( \frac{b}{r} ) $$

Operations on Complex Numbers in Trigonometric Form

Given two complex numbers expressed in trigonometric form:

$$ z_1 = r_1 \cdot ( \cos \alpha + i \sin \alpha ) $$

$$ z_2 = r_2 \cdot ( \cos \beta + i \sin \beta ) $$

several operations become more convenient to perform:

• Multiplication
  The product of two complex numbers in trigonometric form results in a complex number whose modulus is the product of the individual moduli, \( r_1 r_2 \), and whose argument is the sum of the individual arguments, \( \alpha + \beta \): $$ z_1 \cdot z_2 = r_1 r_2 \cdot [ \cos ( \alpha+\beta ) + i \sin ( \alpha+\beta ) ] $$
• Division
  The quotient of two complex numbers in trigonometric form is a complex number whose modulus is the quotient of the individual moduli, \( r_1 / r_2 \), and whose argument is the difference of the individual arguments, \( \alpha - \beta \): $$ \frac{z_1}{z_2} = \frac{r_1}{r_2} \cdot [ \cos ( \alpha-\beta ) + i \sin ( \alpha-\beta ) ] $$
• Reciprocal
  The reciprocal of a complex number in trigonometric form is given by: $$ \frac{1}{z_1} = \frac{1}{r_1} \cdot (\cos \alpha - i \sin \alpha) $$
• Exponentiation
  Raising a complex number to the power of \( n \) results in a complex number whose modulus is raised to the \( n \)th power, i.e., \( r_1^n \), and whose argument is multiplied by \( n \), i.e., \( n \alpha \): $$ z_1^n = r_1^n \cdot [ \cos(n \alpha) + i \sin(n \alpha)] $$

Converting a Complex Number from Trigonometric to Cartesian Form

Converting a complex number from trigonometric form to Cartesian form, \( z = a + bi \), is a straightforward process.

Given a complex number in trigonometric form:

$$ z = r \left( \cos \alpha + i \sin \alpha \right) $$

The Cartesian components \( z = a + bi \) are computed as follows:

$$ a = r \cos \alpha \quad \text{(real part)} $$

$$ b = r \sin \alpha \quad \text{(imaginary part)} $$

Once the values of \( a \) and \( b \) are determined, the complex number can be expressed in Cartesian form as \( z = a + bi \).

Example

Consider the following complex number in trigonometric form:

$$ z = 3 \left( \cos \frac{\pi}{3} + i \sin \frac{\pi}{3} \right) $$

We first compute \( \cos \alpha \) and \( \sin \alpha \) for \( \alpha = \frac{\pi}{3} \):

$$ \cos \frac{\pi}{3} = \frac{1}{2} $$

$$ \sin \frac{\pi}{3} = \frac{\sqrt{3}}{2} $$

Substituting these values into the given complex number:

$$ z = 3 \left( \frac{1}{2} + i \frac{\sqrt{3}}{2} \right) $$

Next, distributing the modulus \( r = 3 \) across both terms:

$$ z = 3 \cdot \frac{1}{2} + 3 \cdot i \frac{\sqrt{3}}{2} $$

$$ z = \frac{3}{2} + i \frac{3\sqrt{3}}{2} $$

Thus, the real part of the complex number is \( a = \frac{3}{2} \), while the imaginary part is \( b = \frac{3\sqrt{3}}{2} \).

Finally, the complex number in Cartesian form is:

$$ z = \frac{3}{2} + i \frac{3\sqrt{3}}{2} $$

And so forth.