Algebraic Form of Complex Numbers

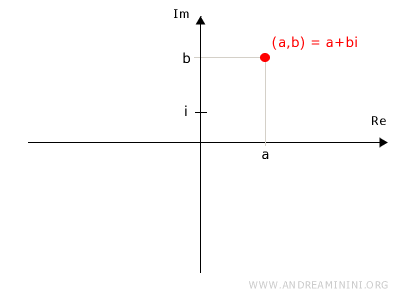
A complex number (a,b) can also be written in its algebraic form as the sum of a real number (a) and an imaginary number (bi): $$ (a,b) = a + b \cdot i $$

Here, $i$ represents the imaginary unit, where \(i = (0,1)\), while \(a\) and \(b\) are real numbers.

The term \(a\) is called the real part, and \(b \cdot i\) is known as the imaginary part of the complex number, with \(b\) being the coefficient of the imaginary part.

The algebraic form is also known as the compact form of complex numbers.

Note: The algebraic form is just one way to represent a complex number. Other representations include the trigonometric form and the exponential form.

If the real part \(a\) is zero, the complex number \(z = a + bi\) is referred to as an imaginary number.

For example, \(z = 3i\) is an imaginary number:

$$ z = 3i $$

Conversely, if the coefficient of the imaginary part is zero (\(b = 0\)), the complex number \(z = a + bi\) is called a real number.

For instance, \(z = 5\) is a real number:

$$ z = 5 $$

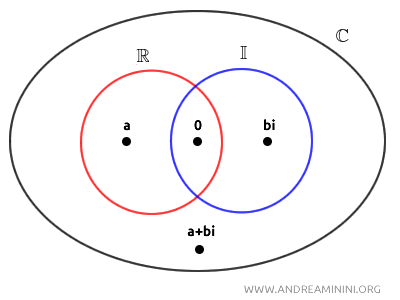
Therefore, the set of complex numbers (\(\mathbb{C}\)) includes both real numbers (\(\mathbb{R}\)) and pure imaginary numbers (\(\mathbb{I}\)) as subsets.

However, it is not merely the union of these subsets—it is a broader set.

Note: The set of complex numbers is larger than the union of real numbers and pure imaginary numbers because it includes all possible combinations of real and imaginary parts. By contrast, the union of real and imaginary numbers only contains cases where either \(a = 0\) or \(b = 0\).

A Practical Example

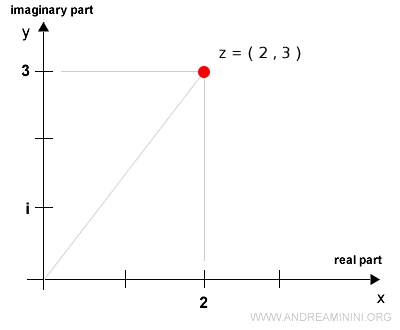
Let’s consider the complex number (2,3):

$$ (a,b) = (2,3) $$

The real part of this complex number is \(a = 2\), while the imaginary part is \(b = 3\).

The algebraic form of the complex number (2,3) is:

$$ (2,3) = 2 + 3i $$

On the Gaussian plane, this corresponds to the same point.

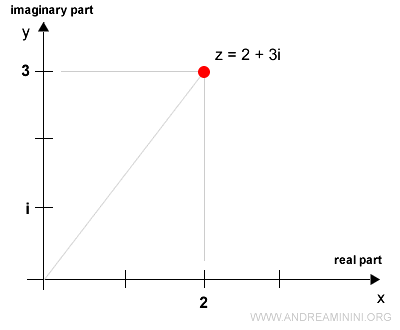
Thus, whether I write (2,3) or \(2 + 3i\), they both represent the same complex number. These are simply two different ways of expressing the same value.

Note: Every point (x, y) on the Gaussian plane corresponds to a complex number, and vice versa. For example, the complex number located at (2,3) can be expressed in algebraic form as \(2 + 3i\).

Operations with Complex Numbers in Algebraic Form

Complex numbers in algebraic form, \(a + bi\), where \(a\) and \(b\) are real numbers and \(i\) is the imaginary unit (\(i^2 = -1\)), follow rules similar to those of binomials.

This means that operations like addition, subtraction, multiplication, and division are governed by principles akin to those of traditional algebra.

Basic Operations with Complex Numbers

• Addition and Subtraction
  Add or subtract the real and imaginary parts separately: $$ (a + bi) + (c + di) = (a + c) + (b + d)i $$ $$
  (a + bi) - (c + di) = (a - c) + (b - d)i $$

  Example: $$ (3 + 2i) + (1 - 4i) = (3 + 1) + (2 - 4)i = 4 - 2i $$

• Multiplication
  Multiply two complex numbers using the distributive property, keeping in mind that \(i^2 = -1\): $$ (a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i
  $$

  Example: $$ (2 + 3i)(1 + 4i) = 2 + 8i + 3i + 12i^2 = 2 + 11i - 12 = -10 + 11i $$

• Conjugate
  The conjugate of a complex number is obtained by changing the sign of the imaginary part: $$ \overline{a + bi} = a - bi $$

  Example: For \(3 + 4i\), the conjugate is \(3 - 4i\).

• Division
  To divide two complex numbers, multiply both numerator and denominator by the conjugate of the denominator: $$ \frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{(c + di)(c - di)} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2} $$

  Example: $$ \frac{3 + 2i}{1 - i} = \frac{(3 + 2i)(1 + i)}{(1 - i)(1 + i)} $$ $$ = \frac{3 + 5i - 2}{2} $$ $$ = 0.5 + 2.5i $$

• Magnitude
  The magnitude (or modulus) of a complex number \(a + bi\) is its distance from the origin on the Gaussian plane, calculated using the Pythagorean theorem: $$ |a + bi| = \sqrt{a^2 + b^2} $$
  

  Example: For \(3 + 4i\), the magnitude is \(\sqrt{3^2 + 4^2} = 5\).

These rules allow me to treat complex numbers as a natural extension of real numbers, simplifying their manipulation and analysis.