Multiplying Complex Numbers in Trigonometric Form

Given two complex numbers in trigonometric form: $$ z= d \cdot ( \cos a + i \cdot \sin a) $$ $$ z'= d' \cdot ( \cos a' + i \cdot \sin a') $$ their product is found by multiplying their moduli and adding their arguments: $$ z \cdot z' = (d \cdot d') \cdot [ \cos(a+a') + i \cdot \sin(a+a') ] $$

A Practical Example

Let's consider two complex numbers:

$$ z=1+3i $$

$$ z'=4+2i $$

Their product is:

$$ z \cdot z' = $$

$$ (1+3i) \cdot (4+2i) = $$

$$ 4 + 2i + 12i +6i^2 = $$

$$ 4 + 14i - 6 = $$

$$ = -2 + 14i $$

Now, let's verify the result using the trigonometric form.

$$ z = 3.16 \cdot ( \cos 71.57° + i \cdot \sin 71.57° ) $$

$$ z' = 4.47 \cdot ( \cos 26.57° + i \cdot \sin 26.57° ) $$

Explanation. The angles are measured in degrees, while \( d \) and \( d' \) represent the magnitudes of the respective complex numbers.

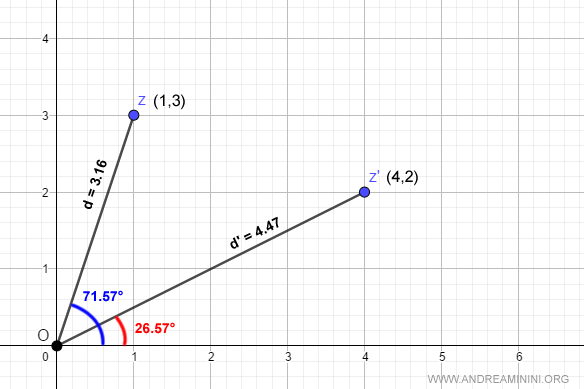
For readability, I've rounded the values of \( d \) and \( d' \): $$ d = \sqrt{1^2+3^2}=\sqrt{10} \approx 3.16 \\ d' = \sqrt{4^2+2^2}=\sqrt{20} \approx 4.47 $$

Applying the multiplication formula for complex numbers in trigonometric form:

$$ z \cdot z' = (d \cdot d') \cdot [ \cos(a+a') + i \cdot \sin(a+a') ] = $$

$$ (3.16 \cdot 4.47) \cdot [ \cos(71.57°+26.57°) + i \cdot \sin(71.57°+26.57°) ] = $$

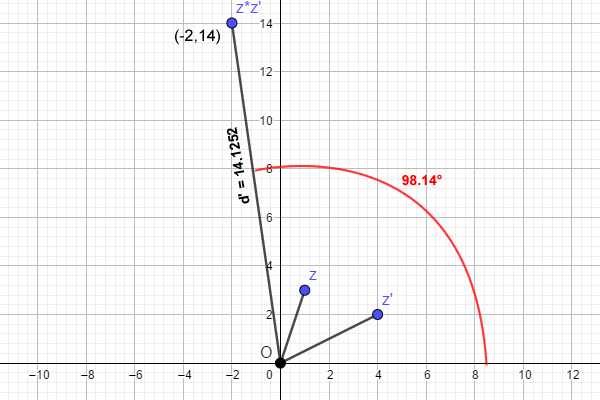
$$ 14.1252 \cdot [ \cos(98.14°) + i \cdot \sin(98.14°) ] = $$

$$ 14.1252 \cdot \cos(98.14°) + 14.1252 \cdot i \cdot \sin(98.14°) = $$

$$ -2 + 14 i $$

As expected, we get the same result!

The Proof

A complex number can also be written in trigonometric form as:

$$ z=x+i \cdot y $$

which is equivalent to:

$$ z= d \cdot ( \cos a + i \cdot \sin a) $$

Now, given two complex numbers \( z \) and \( z' \) in trigonometric form:

$$ z= d \cdot ( \cos a + i \cdot \sin a) $$ $$ z'= d' \cdot ( \cos a' + i \cdot \sin a') $$

Let's compute their product algebraically:

$$ z \cdot z' = $$

$$ d \cdot ( \cos a + i \cdot \sin a) \cdot d' \cdot ( \cos a' + i \cdot \sin a') = $$

$$ (d \cdot d' ) \cdot [ ( \cos a + i \cdot \sin a) \cdot ( \cos a' + i \cdot \sin a') ] = $$

Expanding the expression:

$$ (d \cdot d' ) \cdot [ \cos a \cdot ( \cos a' ) + \cos a \cdot ( i \cdot \sin a' ) + i \cdot \sin a \cdot ( \cos a' ) + i \cdot \sin a \cdot ( i \cdot \sin a') ] = $$

Since \( i^2 = -1 \), we simplify:

$$ (d \cdot d' ) \cdot [ \cos a \cdot \cos a' + i \cdot \cos a \cdot \sin a' + i \cdot \sin a \cdot \cos a' - \sin a \cdot \sin a' ] = $$

Rearranging terms:

$$ (d \cdot d' ) \cdot [ ( \cos a \cdot \cos a' - \sin a \cdot \sin a' ) + i \cdot ( \cos a \cdot \sin a' + \sin a \cdot \cos a' ) ] = $$

Note. From trigonometry, we know the angle sum identities: $$ \sin (A+B) = \sin A \cos B + \cos A \sin B $$ $$ \sin (A-B) = \sin A \cos B - \cos A \sin B $$ $$ \cos(A+B) = \cos A \cos B - \sin A \sin B $$ $$ \cos(A-B) = \cos A \cos B + \sin A \sin B $$

Using these identities, we obtain:

$$ (d \cdot d' ) \cdot [ \cos (a+a') + i \cdot ( \sin(a+a') ] = $$

Thus, we have derived the formula for multiplying complex numbers in trigonometric form.

And so, the proof is complete.