Dividing Complex Numbers in Trigonometric Form

For two complex numbers expressed in trigonometric form: $$ z = d \cdot ( \cos a + i \cdot \sin a ) $$ $$ z' = d' \cdot ( \cos a' + i \cdot \sin a' ) $$ you can derive their quotient using the formula: $$ \frac{z}{z'} = \frac{d}{d'} \cdot [ \cos (a-a') + i \cdot \sin (a-a') ] $$

Working Through an Example

Consider the complex numbers:

$$ z=1+3i $$

$$ z'=4+2i $$

To divide these, apply the formula:

$$ \frac{x+iy}{x'+iy'} = \frac{xx'+yy'}{x'^2+y'^2}+i \cdot \frac{x'y-xy'}{x'^2+y'^2} $$

$$ \frac{z}{z'} = \frac{1+i3}{4+i2} = \frac{1\cdot4+3\cdot2}{4^2+2^2}+i \cdot \frac{4\cdot3-1\cdot2}{4^2+2^2} $$

$$ \frac{4+6}{16+4}+i \cdot \frac{12-2}{16+4} $$

$$ \frac{10}{20}+i \cdot \frac{10}{20} $$

$$ \frac{1}{2}+i \cdot \frac{1}{2} $$

Let's redo the calculation using trigonometric forms:

$$ z = 3.16 \cdot ( \cos 71.57° + i \cdot \sin 71.57° ) $$

$$ z' = 4.47 \cdot ( \cos 26.57° + i \cdot \sin 26.57° ) $$

Explanation: Angles are measured in degrees and the values d and d' represent the magnitudes of the vectors.

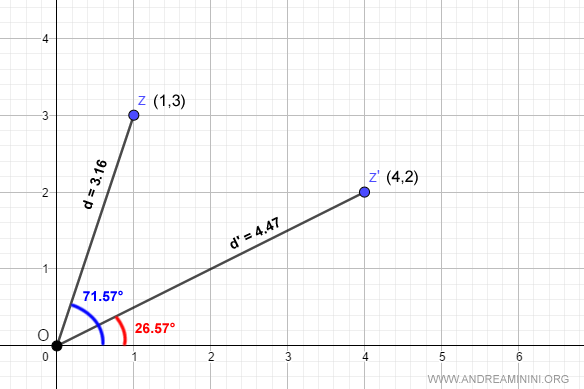
To simplify, we approximate the vector lengths: $$ d = \sqrt{1^2+3^2}=\sqrt{10} ≅ 3.16 \\ d' = \sqrt{4^2+2^2}=\sqrt{20}≅ 4.47 $$

Now, applying the trigonometric division formula:

$$ \frac{z}{z'} = \frac{d}{d'} \cdot [ \cos (71.57°-26.57°) + i \cdot \sin (71.57°-26.57°) ] = $$

$$ 0.706 \cdot [ \cos (45°) + i \cdot \sin (45°) ] = $$

$$ 0.706 \cdot [ 0.70710678118 + i \cdot 0.70710678118 ] = $$

$$ 0.5 + i \cdot 0.5 $$

The outcomes match.

Demonstrating the Formula

Consider two complex numbers given in trigonometric form:

$$ z = d \cdot ( \cos a + i \cdot \sin a ) \\ z' = d' \cdot ( \cos a' + i \cdot \sin a' ) $$

For their division:

$$ \frac{z}{z'} = \frac{ d \cdot ( \cos a + i \cdot \sin a ) }{ d' \cdot ( \cos a' + i \cdot \sin a' ) } \cdot \frac{ d' \cdot ( \cos a' - i \cdot \sin a' ) }{ d' \cdot ( \cos a' - i \cdot \sin a' ) } = $$

Multiplying the numerator and the denominator by the conjugate of the denominator simplifies to:

$$ \frac{ d \cdot ( \cos a + i \cdot \sin a ) }{ d' \cdot ( \cos a' + i \cdot \sin a' ) } \cdot \frac{ ( \cos a' - i \cdot \sin a' ) }{ ( \cos a' - i \cdot \sin a' ) } = $$

$$ \frac{d}{d'} \cdot \frac{ \cos a \cdot \cos a' - \cos a \cdot i \cdot \sin a' + i \cdot \sin a \cdot \cos a' - i^2 \cdot \sin a \cdot \sin a' }{ \cos^2 a' - \cos a' \cdot i \cdot \sin a' + i \cdot \sin a' \cdot \cos a' - i^2 \cdot \sin^2 a' } = $$

With the identity i² = -1:

$$ \frac{d}{d'} \cdot \frac{ \cos a \cdot \cos a' - \cos a \cdot i \cdot \sin a' + i \cdot \sin a \cdot cos a' + \sin a \cdot \sin a' }{ \cos^2 a' - \cos a' \cdot i \cdot sin a' + i \cdot sin a' \cdot \cos a' + \sin^2 a' } = $$

$$ \frac{d}{d'} \cdot \frac{ \cos a \cdot \cos a' - \cos a \cdot i \cdot \sin a' + i \cdot \sin a \cdot \cos a' + \sin a \cdot \sin a' }{ \cos^2 a' + \sin^2 a' } = $$

After applying the trigonometric identities:

$$ \frac{d}{d'} \cdot \frac{ \cos a \cdot \cos a' - \cos a \cdot i \cdot \sin a' + i \cdot \sin a \cdot \cos a' + \sin a \cdot \sin a' }{ 1 } = $$

$$ \frac{d}{d'} \cdot [ \cos a \cdot \cos a' - \cos a \cdot i \cdot \sin a' + i \cdot \sin a \cdot \cos a' + \sin a \cdot \sin a' ] = $$

Note: Trigonometric addition and subtraction formulas dictate: $$ \sin (A+B) = \sin A \cos B + \cos A \sin B $$ $$ \sin (A-B) = \sin A \cos B - \cos A sin B $$ $$ \cos(A+B) = \cos A \cos B - \sin A \sin B $$ $$ \cos(A-B) = \cos A \cos B + \sin A sin B $$

$$ \frac{d}{d'} \cdot [ ( \cos a \cdot \cos a' + \sin a \cdot \sin a' ) + i \cdot ( \sin a \cdot \cos a' - \cos a \cdot \sin a' ) ] = $$

$$ \frac{d}{d'} \cdot [ \cos (a-a') + i \cdot \sin a-a' ]  $$