The n-th Root of Unity

An n-th root of unity is a complex number \( z \) that satisfies the equation: $$ z^n = 1 $$ In other words, raising \( z \) to the power of \( n \) yields 1: $$ \sqrt[n]{z^n} = \sqrt[n]{1} $$ $$ z = \sqrt[n]{1} $$

In trigonometric form, the n-th roots of unity are expressed as:

$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \sin \frac{ 2k \pi }{n} $$

Alternatively, in exponential form:

$$ u_k = e^{\frac{2\pi i k}{n}}, \quad \text{where } k = 0, 1, 2, \ldots, n-1 $$

Understanding Roots of Unity

By definition, an n-th root of unity is a complex number \( u \) that satisfies: $$ u^n = 1 $$ where \( n \) is a positive integer.

Simply put, this means that when \( u \) is raised to the \( n \)th power, it cycles back to 1.

Mathematically, we often express an n-th root of unity using the notation \( \sqrt[n]{1} \), since taking the n-th root of \( u^n = 1 \) is equivalent to taking the n-th root of 1 itself:

$$ \sqrt[n]{u^n} = \sqrt[n]{1} $$

From this, we can rewrite:

$$ u = \sqrt[n]{1} $$

This explains why the complex number \( u \) is called an n-th root of unity.

Finding the Roots of Unity

The n-th roots of unity, denoted as \( u_k = \sqrt[n]{1} \), are given by the following formulas:

• Trigonometric form: $$ u_k = \cos \frac{2k \pi}{n} + i \sin \frac{2k \pi}{n}, \quad \text{for } k = 0, 1, 2, \ldots, n-1 $$
• Exponential form: $$ u_k = e^{\frac{2\pi i k}{n}}, \quad \text{for } k = 0, 1, 2, \ldots, n-1 $$

Here, \( k \) acts as an index that labels each distinct root.

The exponential form \( e^{\frac{2\pi i k}{n}} \) is just a more compact representation of the trigonometric expression.

Note: The exponential form is particularly useful in many mathematical applications—but be warned: trying to compute these values by hand without a calculator is a quick way to lose patience. After a few \( \pi \) terms, you might be tempted to throw your notes out the window!

Geometrically, the roots of unity correspond to the vertices of a regular \( n \)-sided polygon inscribed in the unit circle of the complex plane.

In other words, these roots are points evenly spaced around the unit circle.

How Many Roots of Unity Are There?

In theory, the unit circle contains an infinite number of roots of unity, since it repeats indefinitely. However, for a given \( n \), only \( n \) distinct roots exist.

It can be rigorously proven that there are exactly \( n \) distinct n-th roots of unity, corresponding to values of \( k = 0, 1, \ldots, n-1 \).

$$ u_k = e^{\frac{2\pi i k}{n}}, \quad \text{for } k = 0, 1, 2, \ldots, n-1 $$

When \( n > 2 \), these \( n \) roots are evenly distributed around the unit circle, forming the vertices of a regular \( n \)-gon centered at the origin. One of these vertices always lies at \( (1,0) \) on the real axis.

Thus, the n-th roots of unity serve a dual purpose: they divide the unit circle into \( n \) equal parts and define the vertices of a regular polygon with \( n \) sides.

To gain deeper insight, let's explore a few concrete examples.

Example: The Square Roots of Unity (\( n = 2 \))

For \( n = 2 \), we seek complex numbers \( u \) satisfying:

$$ u^2 = 1 $$

The two solutions are:

1. \( u_0 = e^{\frac{2\pi i \cdot 0}{2}} = e^0 = 1 \)
2. \( u_1 = e^{\frac{2\pi i \cdot 1}{2}} = e^{\pi i} = -1 \)

These two roots lie at opposite points on the unit circle, effectively splitting it into two equal halves.

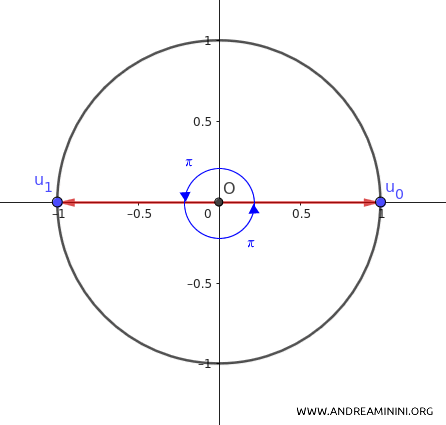
Example: The Cube Roots of Unity (\( n = 3 \))

For \( n = 3 \), we look for complex numbers \( u \) such that:

$$ u^3 = 1 $$

We find three distinct roots:

1. \( u_0 = e^{\frac{2\pi i \cdot 0}{3}} = e^0 = 1 \)
2. \( u_1 = e^{\frac{2\pi i \cdot 1}{3}} = e^{\frac{2\pi i}{3}} \)
3. \( u_2 = e^{\frac{2\pi i \cdot 2}{3}} = e^{\frac{4\pi i}{3}} \)

These roots divide the unit circle into three equal arcs, forming the vertices of an equilateral triangle inscribed in the circle.

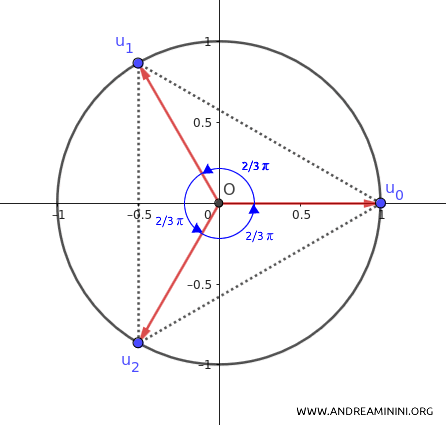
Example: The Fourth Roots of Unity (\( n = 4 \))

For \( n = 4 \), we seek the complex numbers \( u \) that satisfy:

$$ u^4 = 1 $$

There are exactly four distinct roots, which can be expressed in exponential form as:

$$ u_k = e^{\frac{2\pi i k}{4}}, \quad \text{for } k = 0, 1, 2, 3 $$

Computing each root explicitly:

1. \( u_0 = e^{\frac{2\pi i \cdot 0}{4}} = e^0 = 1 \)
2. \( u_1 = e^{\frac{2\pi i \cdot 1}{4}} = e^{\frac{\pi i}{2}} = i \)
3. \( u_2 = e^{\frac{2\pi i \cdot 2}{4}} = e^{\pi i} = -1 \)
4. \( u_3 = e^{\frac{2\pi i \cdot 3}{4}} = e^{\frac{3\pi i}{2}} = -i \)

These four complex numbers represent the vertices of a square inscribed in the unit circle in the complex plane. Each root is spaced evenly around the circle, dividing it into four equal sections.

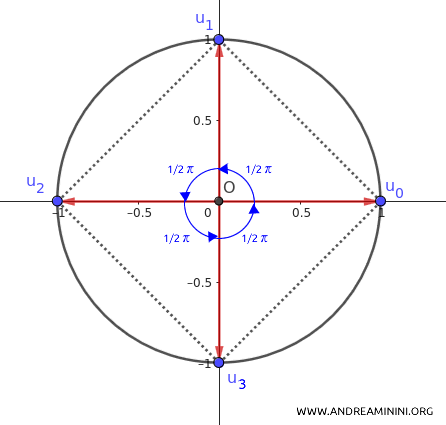
A Practical Example

The square roots of unity correspond to \( n = 2 \) and have exactly two distinct solutions.

For \( k = 0 \), the first solution is:

$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \sin \frac{ 2k \pi }{n} $$

Substituting \( k = 0 \):

$$ \sqrt[2]{1} = \cos \frac{ 2 \cdot 0 \cdot \pi }{2} + i \sin \frac{ 2 \cdot 0 \cdot \pi }{2} $$

$$ \sqrt[2]{1} = \cos 0 + i \sin 0 $$

$$ \sqrt[2]{1} = 1 + i \cdot 0 $$

$$ \sqrt[2]{1} = 1 $$

For \( k = 1 \), the second solution is:

$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \sin \frac{ 2k \pi }{n} $$

Substituting \( k = 1 \):

$$ \sqrt[2]{1} = \cos \frac{ 2 \cdot 1 \cdot \pi }{2} + i \sin \frac{ 2 \cdot 1 \cdot \pi }{2} $$

$$ \sqrt[2]{1} = \cos \frac{ 2\pi }{2} + i \sin \frac{ 2\pi }{2} $$

$$ \sqrt[2]{1} = \cos \pi + i \sin \pi $$

$$ \sqrt[2]{1} = -1 + i \cdot 0 $$

$$ \sqrt[2]{1} = -1 $$

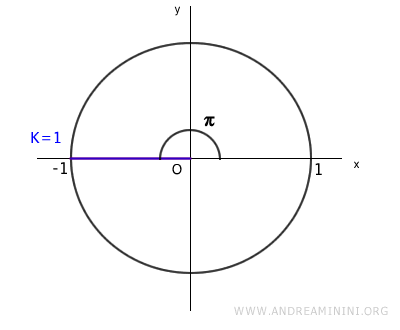
Note: The roots follow a cyclic pattern for \( k > 1 \), alternating between \( 1 \) and \( -1 \). For instance, when \( k = 2 \), the root is \( 1 \); for \( k = 3 \), the root is \( -1 \), and so on. Because of this periodicity, we only consider the first two unique solutions: \( 1 \) and \( -1 \). More generally, for an n-th root of unity, we account for the first \( n \) distinct solutions.

Proof

We start with the fundamental equation:

$$ z^n = 1 $$

Expressing the complex number in its polar form:

$$ [r \cdot ( \cos \alpha + i \sin \alpha) ]^n = 1 $$

Since \( 1 \) can be written in polar form as \( \cos 0 + i \sin 0 \):

$$ [r \cdot ( \cos \alpha + i \sin \alpha) ]^n = \cos 0 + i \sin 0 $$

The modulus on the right-hand side is 1, so we rewrite:

$$ [r \cdot ( \cos \alpha + i \sin \alpha) ]^n = 1 \cdot ( \cos 0 + i \sin 0 ) $$

Applying De Moivre’s theorem for exponentiating complex numbers:

$$ r^n \cdot ( \cos n\alpha + i \sin n\alpha) = 1 \cdot ( \cos 0 + i \sin 0 ) $$

This identity remains valid for integer multiples of \( 2k\pi \):

$$ r^n \cdot ( \cos n\alpha + i \sin n\alpha) = 1 \cdot [ \cos ( 0 + 2k \pi) + i \sin ( 0 + 2k \pi) ] $$

By comparing both sides, we deduce:

$$ \begin{cases} r^n = 1 \\ \\ n \alpha = 0 + 2k \pi \end{cases} $$

Solving for \( \alpha \):

$$ \begin{cases} r^n = 1 \\ \\ \alpha = \frac{ 2k \pi }{n} \end{cases} $$

Thus, the general formula for the n-th roots of unity is:

$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \sin \frac{ 2k \pi }{n} $$

for any integer \( k \).

This proves the formula for the n-th roots of unity.