Modulus of a Complex Number

The modulus of a complex number is a non-negative real number (either positive or zero), defined as the square root of the sum of the squares of its real and imaginary components. It is represented with two vertical bars: $$ |z| = |a+bi| = \sqrt{a^2+b^2} $$. Geometrically, the modulus represents the length of the vector connecting the complex number $(a, b)$ to the origin.
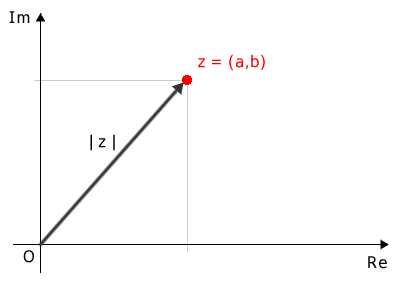
the modulus of the complex number

Here, $a$ and $b$ are real numbers that define the complex number $z = a + bi$.

The term $a$ is the real part, $Re(z) = a$, while $b$ is the coefficient of the imaginary part, $Im(z) = bi$.

Note: The modulus of a vector allows us to apply trigonometry and vector calculus to the study of complex numbers. For example, knowing the modulus and the angle of the vector relative to the x-axis enables the representation of complex numbers in trigonometric and polar forms.

The Geometric Interpretation of the Modulus
A Practical Example

The Geometric Interpretation of the Modulus

A complex number can be viewed as an ordered pair of real numbers:

$$ z = (a, b) $$

In this sense, it corresponds to a point in the Gauss plane.

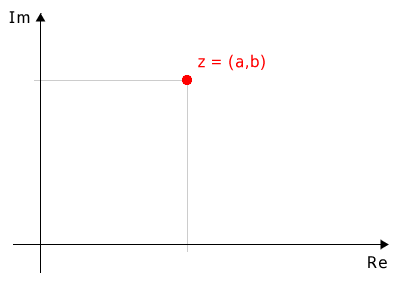
the complex number in the Gauss plane

Every point in the plane represents a complex number, and every complex number corresponds to a point.

Note: In the Gauss plane, the x-coordinate represents real numbers ($Re$), while the y-coordinate represents imaginary numbers ($Im$).

The modulus of a complex number is the length of the directed segment (vector) connecting the origin to the point $(a, b)$.

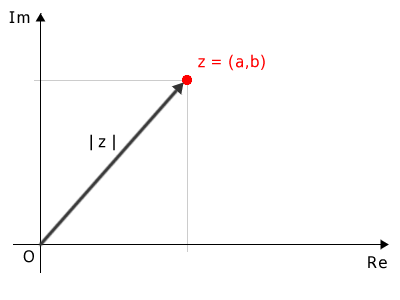
the modulus of the complex number

Projecting this point onto the x-axis (or y-axis) creates a right triangle in the plane.

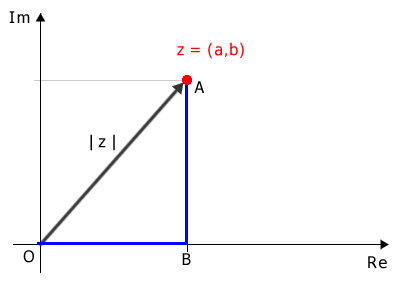
the explanation of the modulus

The legs ($OB$ and $AB$) of this right triangle correspond to the real part ($a$) and the imaginary coefficient ($b$) of the complex number $(a, b)$, respectively:

$$ \overline{OB} = Re(z) = a $$

$$ \overline{AB} = Im(z) = b $$

The hypotenuse ($OA$) represents the modulus of the complex number:

$$ \overline{OA} = |z| $$

Using the Pythagorean theorem, the square of the hypotenuse equals the sum of the squares of the two legs:

$$ |z|^2 = \overline{OA}^2 = \overline{OB}^2 + \overline{AB}^2 $$

Taking the square root of both sides gives:

$$ \sqrt{\overline{OA}^2} = \sqrt{\overline{OB}^2 + \overline{AB}^2} $$

$$ |z| = \overline{OA} = \sqrt{\overline{OB}^2 + \overline{AB}^2} $$

Since $\overline{OB} = Re(z) = a$ and $\overline{AB} = Im(z) = b$:

$$ |z| = \sqrt{\overline{OB}^2 + \overline{AB}^2} = \sqrt{a^2 + b^2} $$

This formula gives the modulus of the complex number $(a, b)$.

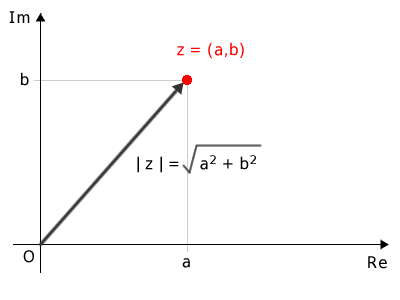
the modulus of the complex number

In summary, the modulus of a complex number is the length of the vector pointing to the coordinates $(a, b)$ in the plane.

The modulus cannot be negative because it represents a length.

In geometry, lengths are always non-negative.

Note: The complex number $(0, 0)$ is the only one with a modulus of zero, as it corresponds to the null vector. All other complex numbers have a positive modulus.

A Practical Example

Let’s consider the complex number:

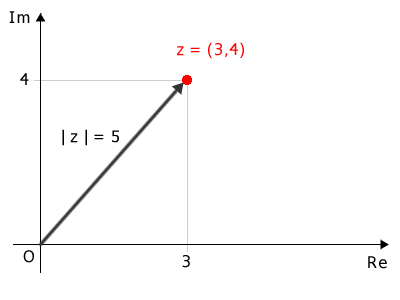
$$ z = (a, b) = (3, 4) $$

The real part of the complex number $(a, b)$ is $a = 3$, and the imaginary coefficient is $b = 4$.

In algebraic form, the complex number can be written as:

$$ z = a + bi = 3 + 4i $$

The modulus of this complex number is 5:

$$ |z| = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} $$ $$ |z| = \sqrt{9 + 16} $$ $$ |z| = \sqrt{25} $$ $$ |z| = 5 $$

The modulus corresponds to the length of the vector connecting the origin of the plane to the point $(3, 4)$.

the modulus of the complex number

And so on.