Exponential Form of Complex Numbers

A complex number can also be expressed in its exponential form: $$ z = r \cdot (\cos \alpha + i \cdot \sin \alpha ) = r \cdot e^{i \cdot \alpha} $$ where \( r \) is the modulus and \( \alpha \) (the argument) lies within the interval \( (0,2\pi) \).

Here, \( e \) is Euler’s number, the base of natural logarithms, approximately \( e = 2.7182... \).

This is known as the exponential representation of a complex number.

Example: A complex number \( z \) in trigonometric form with a unit modulus (\( r=1 \)) and argument \( \alpha \) simplifies to \( e^{i\alpha} \) in exponential form: $$ z = (\cos \alpha + i \cdot \sin \alpha ) = e^{i \alpha} $$

Why Use the Exponential Form?

The exponential form is widely used in applied mathematics, engineering, and physics because it greatly simplifies many operations involving complex numbers.

For example, once the modulus and argument are known, computing the n-th root or the n-th power of a complex number becomes much more straightforward.

Note: The complex conjugate of a number \( z = x + iy \) in exponential form is given by: $$ \overline{z} = r \cdot (\cos \alpha - i \cdot \sin \alpha ) = r \cdot e^{-i \cdot \alpha} $$

Proof

The exponential form of a complex number follows directly from Euler’s formula:

$$ r ( \cos \alpha + i \cdot \sin \alpha) = r \cdot e^{i \cdot \alpha} $$

Euler’s formula provides a bridge between the trigonometric and exponential representations of complex numbers.

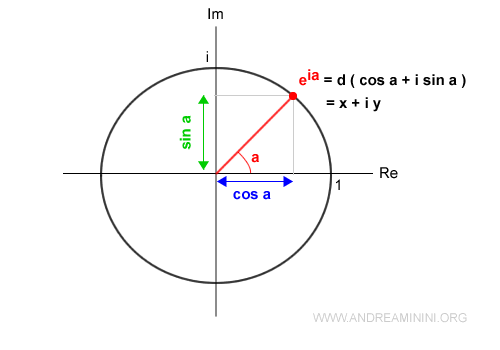
Expressing \( z \) as \( a+bi \), \( r(\cos \alpha + i \sin \alpha) \), or \( r e^{i\alpha} \) all describe the same point \( (x,y) \) in the complex plane.

Converting from Algebraic to Exponential Form

To express a complex number in exponential form, we first rewrite it in polar (trigonometric) form.

Given a complex number in algebraic form:

$$ z = a + bi $$

we need to determine its modulus \( r \) and argument \( \alpha \). Once these are known, converting to exponential form is straightforward.

Example

Consider the complex number:

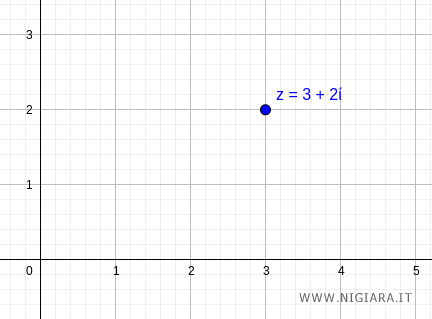
$$ z = 3+2i $$

In the complex plane, this corresponds to the point \( (3,2) \).

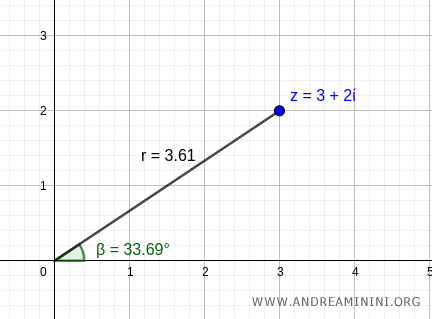
Step 1: Compute the Modulus

The modulus (or absolute value) of \( z \) is given by:

$$ r = \sqrt{3^2+2^2} = \sqrt{9+4} = \sqrt{13} \approx 3.61 $$

Step 2: Compute the Argument

The argument \( \alpha \) (the angle measured counterclockwise from the positive real axis) is given by:

$$ \alpha = \arctan \frac{2}{3} \approx 33.69^\circ $$

Thus, the trigonometric form of \( z \) is:

$$ z = 3.61 \cdot \left( \cos 33.69^\circ + i \sin 33.69^\circ \right) $$

This still represents the same point \( (3,2) \) in the complex plane, but now using polar coordinates \([ 3.61 , 33.69^\circ ]\).

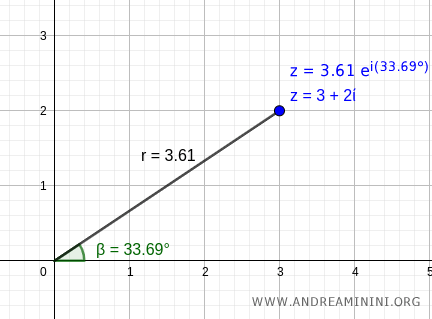
Step 3: Convert to Exponential Form

Using Euler’s formula, we express the complex number in exponential form:

$$ z = r e^{i \alpha} $$

Since we already know \( r = 3.61 \) and \( \alpha = 33.69^\circ \), we can write:

$$ z = 3.61 \cdot e^{i \cdot 33.69^\circ } $$

This exponential form is fully equivalent to the original algebraic form—it represents the same point in the complex plane but provides a more elegant and powerful notation, particularly useful for mathematical operations.

Note: Converting from exponential to trigonometric form is just as straightforward—since both the modulus and argument are already known, no additional computations are needed.

Converting from Exponential to Algebraic Form

To express a complex number in algebraic form, we first rewrite it in trigonometric form and then evaluate the trigonometric functions.

Example

Consider the complex number given in exponential form:

$$ z = 3 \cdot e^{i \frac{\pi}{6} } $$

where the modulus is \( 3 \) and the argument (angle) is \( \frac{\pi}{6} \).

Step 1: Convert to Trigonometric Form

Using Euler’s formula:

$$ e^{i\alpha} = \cos \alpha + i \sin \alpha $$

we rewrite the given complex number as:

$$ z = 3 \cdot \left( \cos \frac{\pi}{6} + i \sin \frac{\pi}{6} \right) $$

Step 2: Evaluate the Trigonometric Functions

From known trigonometric values:

$$ \cos \frac{\pi}{6} = \frac{\sqrt{3}}{2}, \quad \sin \frac{\pi}{6} = \frac{1}{2} $$

we substitute these values:

$$ z = 3 \cdot \left( \frac{\sqrt{3}}{2} + i \cdot \frac{1}{2} \right) $$

Step 3: Expand and Simplify

Distributing the factor of 3:

$$ z = \frac{3\sqrt{3}}{2} + i \cdot \frac{3}{2} $$

This is the algebraic (Cartesian) form of the given complex number:

$$ z = \frac{3\sqrt{3}}{2} + i \frac{3}{2} $$

Geometric Interpretation: In the complex plane, the real part corresponds to the x-coordinate, and the imaginary part corresponds to the y-coordinate: $$ x = \frac{3\sqrt{3}}{2}, \quad y = \frac{3}{2} $$ Thus, the point \( \left( \frac{3\sqrt{3}}{2}, \frac{3}{2} \right) \) represents the same complex number in Cartesian coordinates.

Operations with Complex Numbers in Exponential Form

Given two complex numbers in exponential form:

$$ z_1 = r_1 (\cos \alpha + i \sin \alpha) = r_1 e^{i \alpha} \\ z_2 = r_2 (\cos \beta + i \sin \beta) = r_2 e^{i \beta} $$

Multiplication

Multiplication of complex numbers in exponential form is particularly convenient, as it follows directly from exponentiation rules:

$$ z_1 \cdot z_2 = ( r_1 e^{i \alpha} ) \cdot ( r_2 e^{i \beta} ) = ( r_1 \cdot r_2 ) e^{i(\alpha+\beta)} $$

Thus, the moduli multiply, and the arguments add. This property makes exponentials an extremely powerful representation, especially in physics and engineering applications.

Division

Similarly, division is equally straightforward:

$$ \frac{z_1}{z_2} = \frac{r_1 e^{i \alpha }}{r_2 e^{i \beta}} = \left( \frac{r_1}{r_2} \right) e^{i(\alpha-\beta)} $$

Here, the moduli divide, and the arguments subtract, greatly simplifying calculations compared to Cartesian or trigonometric forms.

Exponentiation

Raising a complex number to an integer power follows naturally from exponentiation rules:

$$ z_1^n = r_1^n e^{i \alpha n } $$

This formula is particularly useful in advanced applications such as electrical circuits, quantum mechanics, and Fourier analysis, where repeated exponentiation of complex numbers is a fundamental operation.

n-th Root

Computing the n-th root of a complex number is significantly easier in exponential form than in Cartesian form:

$$ \sqrt[n]{z_1} = r_1^{\frac{1}{n}} e^{i \frac{\alpha + 2\pi k}{n} }, \quad k = 0, 1, \dots, n-1 $$

The presence of \( 2\pi k \) accounts for the \( n \) distinct roots of the complex number, evenly spaced around the unit circle in the complex plane.

More generally, for any exponent \( m/n \):

$$ \sqrt[n]{z_1^m} = r_1^{\frac{m}{n}} e^{i \frac{m (\alpha + 2\pi k)}{n} } $$

This formula is particularly useful when working with complex roots of unity and periodic functions.

Note: When the modulus and argument of a complex number are known, all these operations can be performed much more efficiently in exponential form than in trigonometric or algebraic form.

Additional Notes

Some key properties of complex numbers in exponential form:

• Two complex numbers \( e^{i \alpha} \) and \( e^{i \beta} \) are equal if their arguments differ by an integer multiple of \( 2\pi \), meaning \( \beta = \alpha + 2 k \pi \). That is: $$ e^{i \alpha} = e^{i \beta} = e^{i (\alpha + 2k \pi)} $$

These properties form the foundation for many concepts in complex analysis, including contour integration, Fourier transforms, and signal processing.