Complex Number Representation
The Cartesian Form
Complex numbers can be represented as coordinates (x, y) on the Cartesian plane: $$ x+yi \equiv P(x,y) $$
A Practical Example
Consider the complex number:
$$ 3+2i $$
Here, \( x = 3 \) and \( y = 2 \), while \( i \) is the imaginary unit.
We can visualize this number as the point \( P(x, y) \) on a two-dimensional Cartesian coordinate system.
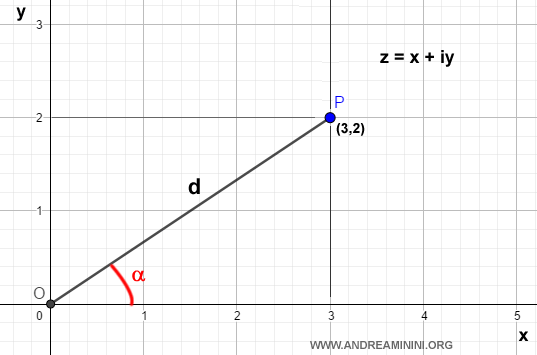
Geometric Interpretation
From a geometric perspective, every complex number can be uniquely described by two values:
- The modulus (or absolute value), which is the length \( d \) of the segment \( OP \).
- The argument (or phase), which is the angle \( \alpha \) formed by the segment \( OP \) with the positive real axis, measured in degrees or radians.
To find the length of \( OP \)—which represents the distance between the point \( P(x,y) \) and the origin \( O(0,0) \)—we apply the Pythagorean theorem:
$$ d = \sqrt{x^2+y^2} $$
The argument \( \alpha \) can be determined using trigonometric ratios:
$$ \cos \alpha = \frac{x}{d}, \quad \sin \alpha = \frac{y}{d} $$
Derivation: The projection of \( P(x,y) \) onto the real axis is given by:
$$ x = d \cos \alpha \quad \Rightarrow \quad \cos \alpha = \frac{x}{d} $$
Similarly, the projection onto the imaginary axis is:
$$ y = d \sin \alpha \quad \Rightarrow \quad \sin \alpha = \frac{y}{d} $$
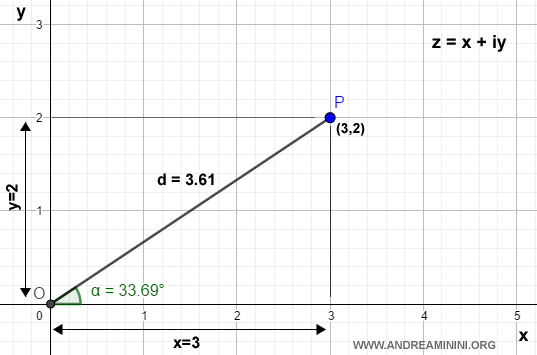
Worked Example
Consider the complex number:
$$ 3+2i $$
This corresponds to the point \( P(3,2) \) on the Cartesian plane.

To find the modulus:
$$ d = \sqrt{3^2 + 2^2} = \sqrt{9 + 4} = \sqrt{13} \approx 3.61 $$
The argument \( \alpha \) is found by computing:
$$ \cos \alpha = \frac{x}{d} = \frac{3}{3.61} \approx 0.83 $$
Taking the inverse cosine:
$$ \alpha = \arccos(0.83) \approx 33.69^\circ $$
Thus, the complex number \( 3+2i \) has an argument of approximately \( 33.69^\circ \).
Note: The argument can also be determined using the sine function:
$$ \sin \alpha = \frac{y}{d} $$
This alternative approach offers another way to compute \( \alpha \), reinforcing the connection between Cartesian and polar representations.
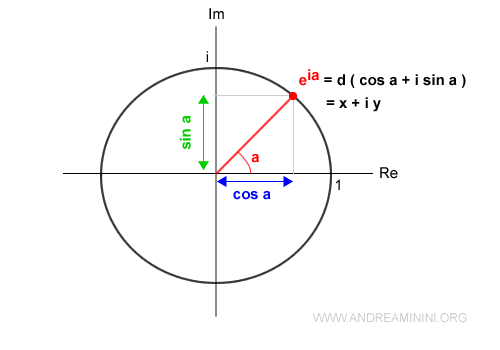
Trigonometric (or Polar) Form
A complex number can also be expressed in trigonometric (or polar) form:
$$ x+yi \equiv d ( \cos \alpha + i \sin \alpha ) $$
This is known as the polar representation because it relies on polar coordinates:
$$ ( d, \alpha ) $$
where \( d \) is the modulus (distance from the origin) and \( \alpha \) is the argument (angle relative to the positive real axis).
Derivation
Starting from the Cartesian form:
$$ z = x+yi $$
We substitute:
$$ x = d \cos \alpha, \quad y = d \sin \alpha $$
which leads to:
$$ z = d \cos \alpha + i ( d \sin \alpha ) $$
or, more compactly:
$$ z = d ( \cos \alpha + i \sin \alpha ) $$
Verification: Using our previous example where \( d = 3.61 \), \( \cos \alpha \approx 0.83 \), and \( \sin \alpha \approx 0.55 \):
$$ x = d \cos \alpha = 3.61 \times 0.83 = 3 $$
$$ y = d \sin \alpha = 3.61 \times 0.55 = 2 $$
These values confirm that the trigonometric form correctly represents the original complex number.
Exponential Form
A complex number can also be written in exponential form:
$$ z = d (\cos \alpha + i \sin \alpha) = d e^{i\alpha} $$
where \( \alpha \) is the argument and lies in the interval \( (0, 2\pi) \).
This is known as the exponential representation.
It is derived from Euler's formula:
$$ e^{i \alpha} = \cos \alpha + i \sin \alpha $$
which allows trigonometric functions to be expressed in terms of the exponential function.
Note: The complex conjugate of \( z = x + iy \) in exponential form is given by:
$$ z^* = d (\cos \alpha - i \sin \alpha) = d e^{-i\alpha} $$
Example
In trigonometric form:
$$ z = 3.61 ( \cos 33.69^\circ + i \sin 33.69^\circ ) $$
The equivalent exponential form is:
$$ z = 3.61 e^{i 33.69^\circ} $$
Why Use the Exponential Form? The exponential representation is particularly useful in mathematical operations where the modulus and argument are more significant than the real and imaginary components. It simplifies multiplication, division, and powers of complex numbers.
