Algebraic Structures
Defining an Algebraic Structure
An algebraic structure consists of a set S along with one or more operations defined on S. $$ (S,*) $$
If it features just one operation, it's called a groupoid.
If the operation in a groupoid is associative, we refer to it as a semigroup.
When a semigroup includes an identity element, it qualifies as a monoid.
What Constitutes an Operation?
An operation is a function that associates elements of set S to other elements within the same set.
$$ *: S \rightarrow S $$
This is termed a binary operation when it involves pairing elements of S to produce another element from S.
$$ *: S×S \rightarrow S $$
An Example of an Algebraic Structure
Example 1
Let's take the set of integers Z with addition (+) as the operation.
$$ ( Z , + ) $$
This setup forms an algebraic structure where each pair of integers (addends) corresponds to another integer (the sum).
$$ +: ZxZ \rightarrow Z $$
Note: If the results of the operation were outside the set Z, it wouldn’t be an algebraic structure.
Example 2
Consider the set of numbers from 1 to 10 with multiplication (*) as the operation.
$$ S = ( 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ) $$
Here, (S,*) fails to form an algebraic structure since some products do not remain within the set S.
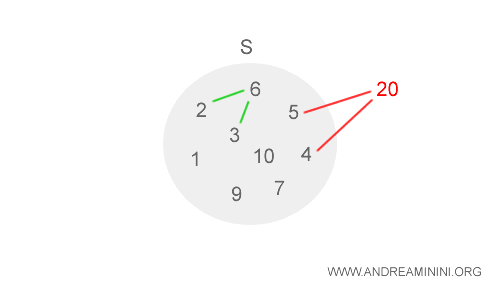
For instance, multiplying 4 and 5 yields 20, which is not an element of S.
$$ (1*2)=2 \\ (2*3)=6 \\ (4*5)=20 $$
This does not meet the criteria for an algebraic structure.
A single set S can be an algebraic structure under one operation and not under another. For example, the set of natural numbers N forms an algebraic structure (N,+) with addition but not with subtraction (N,-), because subtracting two natural numbers could result in a negative number, which is outside the set.
The Truth Table
Creating an algebraic structure with a finite number of elements allows for its representation via a truth table.
Example
I have a set S composed of three elements {a,b,c} and an operation |
$$ (S,|) $$
The operation links each pair of elements in SxS to another element within S.
Here is the truth table:
| a | b | c | |
|---|---|---|---|
| a | a | a | b |
| b | c | b | a |
| c | a | b | c |
This represents a simple algebraic structure, specifically a groupoid, with just one operation.
And so on.
Important Note. The logic used to associate pairs of elements with outcomes is not predetermined. For example, the result of (a,b) could logically be c, a, or b. The outcome depends on the chosen function or the logical circuit. The essential criterion for an algebraic structure is that the result also belongs to the set S.
