Quasigroups

A quasigroup is a groupoid (S,*) that guarantees the existence of both a right inverse (d_x) and a left inverse (s_x) for every pair of elements a and b, satisfying the equations $$ a*d_x=b $$ and $$ s_x*a=b $$.

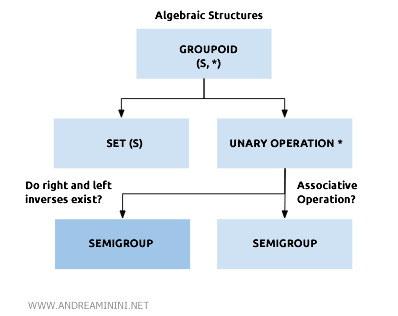
Quasigroups belong to a broader category of groupoids.

This means every quasigroup is a groupoid, but does not necessarily have commutative inverses.

If a quasigroup also contains the neutral element for its operation, it is known as a loop.

An Applied Example

The set of all integers Z under the operation of subtraction (-) forms a quasigroup (Z,-).

$$ (Z,-) $$

We will now review the properties of this algebraic structure.

Subtraction is a closed operation within the set of integers Z, as the difference between any two integers results in another integer.

$$ \forall a,b \in Z \Longrightarrow a-b \in Z $$

Thus, the structure (Z,-) qualifies as a groupoid.

Example: Consider integers a=4 and b=7; their difference is $$ a-b=4-7=-3 $$, another integer.

Every pair of integers a and b has both a right and a left inverse.

Consequently, the structure (Z,-) is a quasigroup.

Example: For the integers a=4 and b=7, the right inverse x=-3 fulfills $$ a-x = b $$ $$ 4-x = 7 $$ $$ x = 4-7 $$ $$ x=-3 $$, while the left inverse y=11 satisfies $$ y-a=b $$ $$ y-4=7 $$ $$ y-4=7 $$ $$ y=7+4 $$ $$ y=11 $$.

And so forth.