Symmetric Groups

A symmetric group (S_n,*) for a set S consists of the set S_n of all permutations of the elements of S, combined with the binary operation of function composition f*g=f o g=f[g).

In this context, each permutation is seen as a bijective function, or correspondence σ, from the set S to itself.

$$ \sigma : S \rightarrow S $$

The set S_n includes all bijective correspondences from the set S to itself.

$$ S_n = \{ \sigma_1, \sigma_2 , ... , \sigma_k \} $$

The symmetric group (S_n,*) is a group of order k=n! because it includes n! possible permutations of n elements in a finite set S.

Note: Symmetric groups of finite sets with the same number of elements (n) are isomorphic. Moreover, all groups with more than two elements are non-abelian (non-commutative).

A Practical Example

Consider a set with three elements (n=3).

$$ S = \{ 1,2,3 \} $$

There are n!=3·2·1=6 possible permutations of these elements.

$$ S_n = \begin{Bmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \\ 2 & 1 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \\ 3 & 2 & 1 \end{Bmatrix} $$

If we start with the set S={1,2,3}, one possible permutation, or bijective correspondence σ, is:

$$ \sigma : (1,2,3) \rightarrow (2,3,1) $$

Tabular notation is used to represent this bijective correspondence σ:

$$ \sigma = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$

Each column of this matrix indicates a relationship S→S within the set itself.

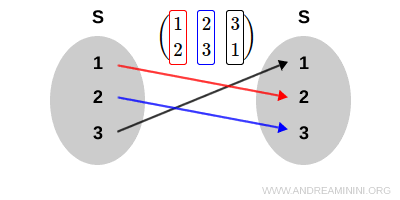
Note: The operation of σ is as follows: $$ \sigma : 1 \rightarrow 2 \\ \sigma : 2 \rightarrow 3 \\ \sigma : 3 \rightarrow 1 $$ This mapping is bijective, meaning for example, σ(1)=3 as 1→2 and 2→3, and σ(3)=1 as 3→1.

The collection of these bijective correspondences σ forms a symmetric group (S_n,*) under the operation of composition *.

$$ (S_n, *) $$

Note: The symmetric group (S_n,*) is of order n!=6 since the set S_n contains 6 elements (its cardinality). $$ S_n = \begin{Bmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \\ 2 & 1 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \\ 3 & 2 & 1 \end{Bmatrix} $$

The composition operation * is a binary operation between two permutations, i.e., between two elements of S_n.

For example, consider two permutations:

$$ \sigma_1 : (1,2,3) \rightarrow (2,1,3) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} $$

$$ \sigma_2 : (1,2,3) \rightarrow (2,3,1) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$

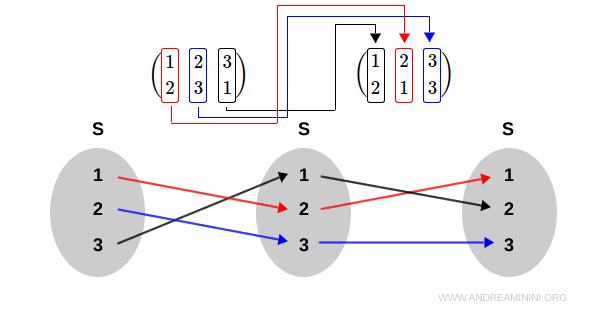
The composition of these permutations is as follows:

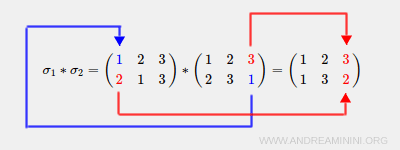
$$ \sigma_1 * \sigma_2 = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} \ $$

Composition must be performed from the rightmost function inward, using f*g=f[g] where g=σ₂ and f=σ₁.

$$ \sigma_1 * \sigma_2 = σ_1 [ σ_2 ] = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} \ $$

The outcome of this composition operation is (1,3,2).

$$ \sigma_1 * \sigma_2 =\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix} $$

A graphical representation should help clarify these steps.

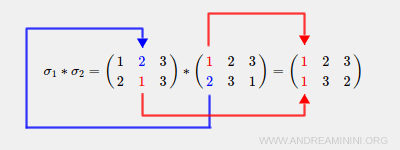
Explanation. The bijective correspondence σ₂ (inner function g) maps 1→2 while σ₁ (outer function f) maps 2→1. Consequently, the composition operation σ₁*σ₂ maps 1→1.

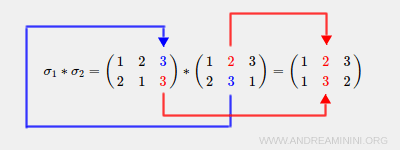
The bijective correspondence σ₂ maps 2→3 while σ₁ maps 3→3. Consequently, the composition operation σ₁*σ₂ maps 2→3.

The bijective correspondence σ₂ maps 3→1 while σ₁ maps 1→2. Consequently, the composition operation σ₁*σ₂ maps 3→2.

Is it an abelian or non-abelian group?

The symmetric group (S_n,*) is composed of permutations of the elements of set S and is structured around the composition operation.

The group has a cardinality of n=3, and thus, being greater than two, the symmetric group is definitively a non-abelian group, lacking the commutative property.

Verification. Revisiting the previous composition which resulted in the permutation (1,3,2) $$ \sigma_1 * \sigma_2 =\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 \\ \color{red} 1 & \color{red} 3 & \color{red} 2 \end{pmatrix} $$ Reversing the composition order yields a different result, (3,2,1) $$ \sigma_2 * \sigma_1 =\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 \\ \color{red} 3 & \color{red} 2 & \color{red} 1 \end{pmatrix} $$ Thus, the group (S_n,*) does not meet the commutative property $$ \sigma_1 * \sigma_2 \ne \sigma_2 * \sigma_1 $$ It is non-abelian.

And so forth