Cyclic Groups
A group (G,*) is called a cyclic group if there exists an element g∈G (known as the generator) that can produce every element in the group G.
In multiplicative cyclic groups, the set G is the set of all powers of the generator element (g):
$$ G = \{ g^n \ : \ n \in \mathbb{Z} \ \} $$
where n is an integer.
In additive cyclic groups, on the other hand, the set G is the set of all multiples of the generator element (g):
$$ G = \{ g \cdot n \ : \ n \in \mathbb{Z} \ \} $$
Note: In cyclic groups, the set G is essentially equal to the subgroup <g> generated by the element g: $$ G = <g> = \{ g^1, ..., g^n \} $$ where gn is the identity element of the group.
The order of the generator is the smallest integer n such that the generator gn equals the identity element (u) of the group:
$$ g^n = u $$
If no such number n exists, then the generator has infinite order.
A Practical Example
The group consisting of the finite set of integers Z4={0,1,2,3} in modular arithmetic, together with the operation of addition, is a cyclic group:
$$ (Z_4, +) $$
This is because there is an element (g=1) in Z4 that can generate all the elements of G:
$$ g = 1 $$
In this case, the generator element is the number 1.
$$ 1^1 = 1 $$ $$ 1^2 = 1+1 = 2 $$ $$ 1^3 = 1+1+1 = 3 $$ $$ 1^4 = 1+1+1+1 = 0 $$
The period of the element 1 is 4 because it takes 4 repetitions of the operation to return to the identity element (e=0) of the group.
Note: For the group (Z4,+), the expression 13 should be interpreted as the group operation (in this case, addition +) repeated three times: 13 = 1+1+1 on the element 1. It’s not an algebraic exponentiation.
The subgroup <1> generated by the element 1 coincides with the set G:
$$ <1> = \{ 0,1,2,3 \} = G $$
The subgroup <1> has a cardinality of 4 because it contains 4 elements.
Thus, the subgroup <1> has an order of 4.
The element 2, however, is not a generator because its multiples (powers) do not generate all the other elements of the set Z4:
$$ 2^0 = 0 $$ $$ 2^1 = 2 $$ $$ 2^2 = 2+2 = 0 $$
The period of the element 2 is 2 because it takes two operations to return to the identity element of the group (e=0).
The subgroup <2> generated by the element 2 contains only two elements, so the subgroup has an order of 2:
$$ <2> = \{ 0,2 \}$$
Note: The period of the element 2 and the order of the subgroup <2> are identical. The subgroup <2> has an order of 2 because it contains two elements (0 and 2). The period of 2 is 2 because the smallest integer k such that gk=0, where the power of the generator g=2 equals the identity element (e), is k=2: $$ 2^2 = 2 + 2 = 0 $$
The element 3 is also a generator of the cyclic group
$$ 3^1 = 3 $$ $$ 3^2 = 3+3 = 2 $$ $$ 3^3 = 3+3 + 3 = 1 $$ $$ 3^4 = 3+3+3+3 = 0 $$
because the subgroup <3> generated by the element 3 coincides with the set G:
$$ <3> = \{ 0,1,2,3 \} = G $$
The subgroup <3> has an order of 4 because it contains 4 elements.
The period of the element 3 is 4 because it takes four repetitions of the operation to return to the identity element e=0 of the group.
Note: The element 0 is not considered a generator, as it is the identity element of the group (Z4,+): $$ 0^1 = 0 $$ $$ 0^2 = 0+0 = 0 $$
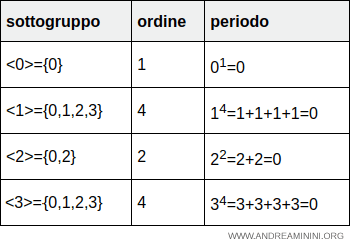
Therefore, the subgroups generated by the elements of the group (Z4,+) are:
| Subgroup | Order | Period |
|---|---|---|
| <0>={0} | 1 | 01=0 |
| <1>={0,1,2,3} | 4 | 14=1+1+1+1=0 |
| <2>={0,2} | 2 | 22=2+2=0 |
| <3>={0,1,2,3} | 4 | 34=3+3+3+3=0 |
Among these, only the subgroups generated by the elements 1 and 3 coincide with the group Z4:
$$ <1>=<3>= \{ 0,1,2,3 \}=Z_4 $$
Therefore, the elements 1 and 3 are generators of the cyclic group (Z4,+).
Properties of Cyclic Groups
Some properties of cyclic groups include:
- Cyclic groups are also Abelian groups (commutative groups).
- If (G,*) is a cyclic group, then its subgroups are also cyclic groups.
Example: The group (Z4,+) is a cyclic group of order n=4 and has the following subgroups:
All its subgroups are also cyclic groups. They all include the identity element (e=0) and return to the identity element after a finite number of operations (periods). - Every finite cyclic group of order n is isomorphic to the group Zn of integers modulo n.
- If (G,*) is a finite cyclic group of order n, an element m∈G can be a generator of G if and only if m and n are coprime integers, meaning GCD(n,m)=1.
Example: The group (Z4,+) is a cyclic group of order n=4. It has two generator elements, 1 and 3. The elements m=1 and m=3 are both coprime to n: GCD(1,4)=1 and GCD(3,4)=1.

- Cauchy’s Theorem
If (G,*) is a finite cyclic group of order n and p is a prime number that divides n, then G contains an element of order p. - Corollary to Cauchy’s Theorem
If the order n of a finite group (G,*) is a prime number, then the group is cyclic. - Every infinite cyclic group is isomorphic to the group (Z,+) of integers under addition, with the element 1 as the generator.
And so on.
