Discrete Logarithms
The discrete logarithm is a variant of the traditional logarithm, used when working with integers in a finite field or a finite group.
More formally, if \( G \) is a cyclic group of order \( n \) and \( g \) is a generator of \( G \), then for any element \( a \) in \( G \), the discrete logarithm \( x \) is the integer satisfying:
\[ g^x \equiv a \mod n \]
where \( x \) lies in the range \( 0 \) to \( n-1 \).
Every element in \( G \) can be expressed as \( g^k \) for some integer \( k \).
The discrete logarithm of an element \( a \) with base \( g \), denoted as logg(a), is the exponent \( x \) such that \( g^x = a \) within the group.
What is it used for? Discrete logarithms are widely used in number theory and cryptography. They are computationally hard to solve, making them a key component of many "one-way functions" in cryptographic systems. While computing \( g^x \mod n \) is straightforward, the inverse operation - solving for \( x \) in \( g^x = y \mod n \), or equivalently \( x = \log_g(y) \mod n \) - is extremely difficult. This asymmetry is the foundation of many cryptographic protocols.
A Practical Example
Let’s consider a cyclic group over a finite field with 11 elements, where arithmetic is performed modulo 11.
$$ G = (1,2,3,4,5,6,7,8,9,10,11) $$
In this system, \( 10 + 1 \mod 11 \) equals 11, but \( 11 + 1 \mod 11 \) wraps back around to 1, since modular arithmetic cycles through the available values.
We can also compute powers within this group:
$$ 2^1 \mod 11 = 2 $$
$$ 2^2 \mod 11 = 4 $$
$$ 2^3 \mod 11 = 8 $$
$$ 2^4 \mod 11 = 5 $$
Note: In standard integer arithmetic, \( 2^4 = 16 \), but since 16 is not within our group modulo 11, we reduce it: \( 16 - 11 = 5 \).
Now, let’s determine the discrete logarithm of 9 with base 2 modulo 11. That means finding \( x \) such that:
$$ 2^x \equiv 9 \mod 11 $$
To solve this, we need to identify the exponent \( x \) for which \( 2^x \) equals 9 modulo 11.
Since we’re working with small numbers, we can solve it by trial:
$$ 2^1 \mod 11 = 2 $$
$$ 2^2 \mod 11 = 4 $$
$$ 2^3 \mod 11 = 8 $$
$$ 2^4 \mod 11 = 5 $$
$$ 2^5 \mod 11 = 10 $$
$$ 2^6 \mod 11 = 9 $$
Thus, the discrete logarithm of 9 with base 2 modulo 11 is 6.
Verification: In standard arithmetic, \( 2^6 = 64 \). In modular arithmetic (mod 11), 64 is equivalent to 9. To confirm this, we can construct the multiplication table for the cyclic group. In this table, multiplying \( 8 \times 8 \mod 11 \) results in 9, verifying our solution.
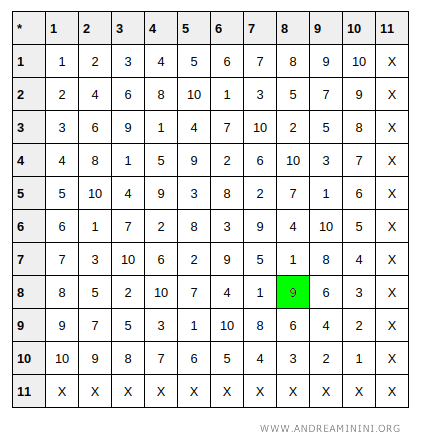
This example illustrates how the discrete logarithm works.
It also highlights why, while verifying \( 2^6 = 9 \mod 11 \) is simple, actually solving for \( x \) becomes significantly harder as numbers grow larger - especially in cryptographic applications.
And so on.
