Modular Arithmetic
What is Modular Arithmetic?
Modular arithmetic is a branch of mathematics that deals with integer calculations within a fixed modulus.
It’s often called clock arithmetic because numbers "wrap around" when they reach the modulus (or a multiple of it), just like the hands of a clock.
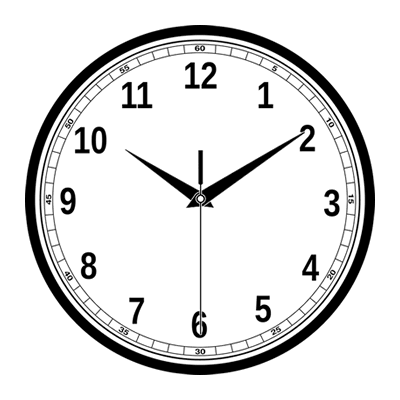
Just as a clock resets to 0 after reaching 12, numbers in modular arithmetic start over once they surpass the modulus.
Who invented it? Modular arithmetic was introduced by Carl Friedrich Gauss in 1801 in his work Disquisitiones Arithmeticae.
A Practical Example
Consider a set \( S \) containing 10 integers: { 0,1,2,3,4,5,6,7,8,9 }.
In standard arithmetic, adding 5 and 5 gives 10:
$$ 5+5 = 10 $$
However, in modular arithmetic, 10 isn’t included in set \( S \).
Instead, the result is 0 because the count resets after reaching the modulus.
$$ 5+5 = 0 $$
This happens because \( S \) is a finite set containing only 10 numbers.
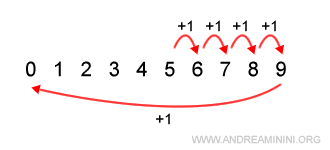
In this case, the modulus is 10:
$$ \mod 10 $$
Note: You can define modular arithmetic with any modulus—8, 6, or any other value. The concept remains the same.
There is a direct equivalence between standard decimal arithmetic and modular arithmetic with modulus 10:
$$ 10 \equiv 0 \mod 10 $$
Using the same principle, we can compute other sums in modular arithmetic:
$$ 5+6=1 \\ 5+7=2 \\ 5+8=3 $$
Note: This applies to any multiple of the modulus and to all arithmetic operations, including addition and subtraction.
To illustrate this further, here’s the addition table for modular addition:
| a+b | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 |
| 5 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 |
| 6 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 |
| 7 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 8 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 9 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Using the same approach, you can construct a subtraction table for modulo 10, or explore other moduli and operations.
Congruences in Modular Arithmetic
Two numbers are congruent if they leave the same remainder when divided by \( m \).
Example
20 and 5 are congruent modulo 3:
$$ 20 \equiv 5 \mod 3 \Rightarrow \begin{cases} \frac{20}{3} = 6 \text{ remainder } 2 \\ \frac{5}{3} = 1 \text{ remainder } 2 \end{cases} $$
Both numbers leave a remainder of 2 when divided by 3:
$ 20 \div 3 = 6 $ with remainder $ r = 2 $
$ 5 \div 3 = 1 $ with remainder $ r = 2 $
And so on.
